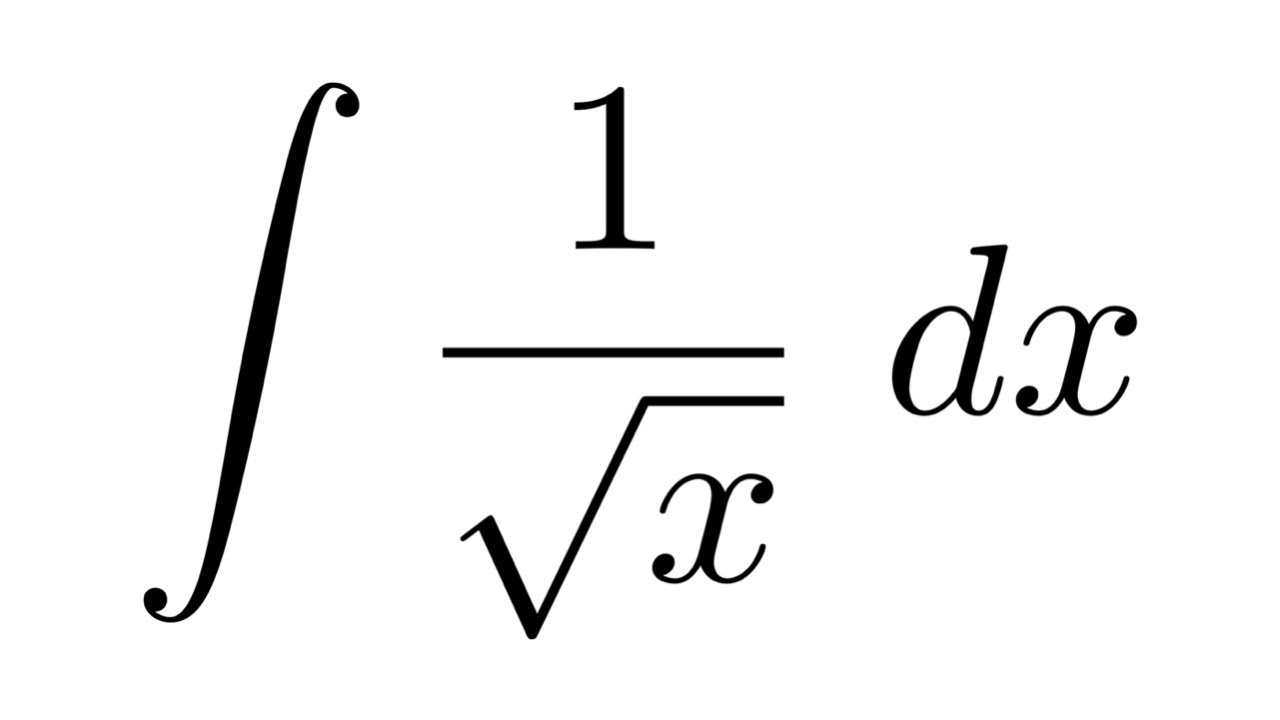Calcular integrales puede parecer un reto, pero en realidad, es más como resolver un rompecabezas. Si alguna vez te has preguntado cómo se hace la integral de 1 sobre la raíz de x, estás en el lugar correcto. En este artículo, desglosaremos el proceso paso a paso, haciéndolo tan sencillo como un paseo por el parque. La integral de 1 sobre la raíz de x es un caso clásico en cálculo, y comprender cómo abordarla puede abrirte las puertas a conceptos más avanzados. ¡Así que vamos a sumergirnos en el tema!
Entendiendo la Integral
Antes de lanzarnos a los cálculos, es esencial entender qué significa realmente la integral de 1 sobre la raíz de x. La función que estamos considerando es f(x) = 1/√x. La integral nos ayuda a encontrar el área bajo la curva de esta función en un intervalo determinado. Pero, ¿por qué es importante esto? Imagina que estás tratando de medir la cantidad de pintura necesaria para cubrir una pared de forma irregular. La integral te ayuda a calcular esa área de manera precisa.
Preparación: Reglas Básicas
Ahora que tenemos una idea de lo que estamos haciendo, hablemos de algunas reglas básicas que necesitamos recordar. La integral de una función f(x) se denota como ∫f(x)dx. En nuestro caso, queremos calcular ∫(1/√x)dx. Para resolverlo, vamos a utilizar una regla fundamental de las integrales: la regla de potencias. ¿Recuerdas cómo funciona?
La Regla de Potencias
La regla de potencias dice que si tienes una función en la forma x^n, la integral se calcula como:
∫x^n dx = (x^(n+1))/(n+1) + C,
donde C es la constante de integración. Ahora, aquí está el truco: tenemos que reescribir nuestra función 1/√x en la forma de la regla de potencias. ¿Listo para ello?
Transformando la Función
La raíz cuadrada de x puede ser expresada como x^(1/2). Por lo tanto, 1/√x se convierte en x^(-1/2). Esto es clave, ya que ahora podemos aplicar la regla de potencias directamente a nuestra función. Así que nuestra integral ahora se ve así:
∫x^(-1/2)dx.
Aplicando la Regla de Potencias
Con nuestra función reescrita, ahora podemos aplicar la regla de potencias. Recuerda que estamos sumando 1 al exponente y dividiendo por el nuevo exponente:
∫x^(-1/2)dx = (x^(-1/2 + 1))/(-1/2 + 1) + C.
Esto simplifica a:
∫x^(-1/2)dx = (x^(1/2))/(1/2) + C.
¿Ves cómo funciona? Ahora tenemos que simplificar esto un poco más. Al dividir por 1/2, es lo mismo que multiplicar por 2, así que:
∫x^(-1/2)dx = 2√x + C.
Y ahí lo tienes, la integral de 1 sobre la raíz de x se calcula como:
∫(1/√x)dx = 2√x + C.
Ahora, ¿no es genial? Has aprendido a calcular esta integral paso a paso, y estoy seguro de que puedes aplicarlo a otros problemas similares. Pero antes de que te vayas, aquí hay algunas preguntas frecuentes que pueden ayudarte aún más.
¿Qué es la constante de integración C?
La constante de integración C es un término que se añade a la integral indefinida. Representa todas las posibles funciones que tienen la misma derivada. En otras palabras, hay infinitas funciones que podrían derivarse para obtener la misma función original.
¿Cómo puedo verificar mi respuesta?
Una buena manera de verificar tu respuesta es derivar la función que obtuviste. Si la derivada coincide con la función original (1/√x), entonces has hecho el trabajo correctamente.
¿Existen otras formas de calcular integrales similares?
¡Absolutamente! Hay métodos como la sustitución u otras técnicas que pueden facilitar el proceso dependiendo de la función que estés tratando de integrar. Siempre es bueno tener varias herramientas en tu caja de herramientas matemática.
¿Por qué es importante aprender a calcular integrales?
Las integrales son fundamentales en muchas áreas de las matemáticas y la ciencia, desde la física hasta la economía. Te ayudan a entender conceptos como el área, el volumen y muchas otras aplicaciones prácticas en el mundo real.
¿Puedo aplicar esto a funciones más complejas?
Definitivamente. Una vez que domines la integral de 1 sobre la raíz de x, puedes aplicar los mismos principios a funciones más complejas. Solo recuerda que la práctica hace al maestro.
Así que ahí lo tienes, una guía completa para calcular la integral de 1 sobre la raíz de x. Espero que hayas encontrado útil esta explicación y que ahora te sientas más cómodo con el cálculo de integrales. ¡Sigue practicando y divirtiéndote con las matemáticas!