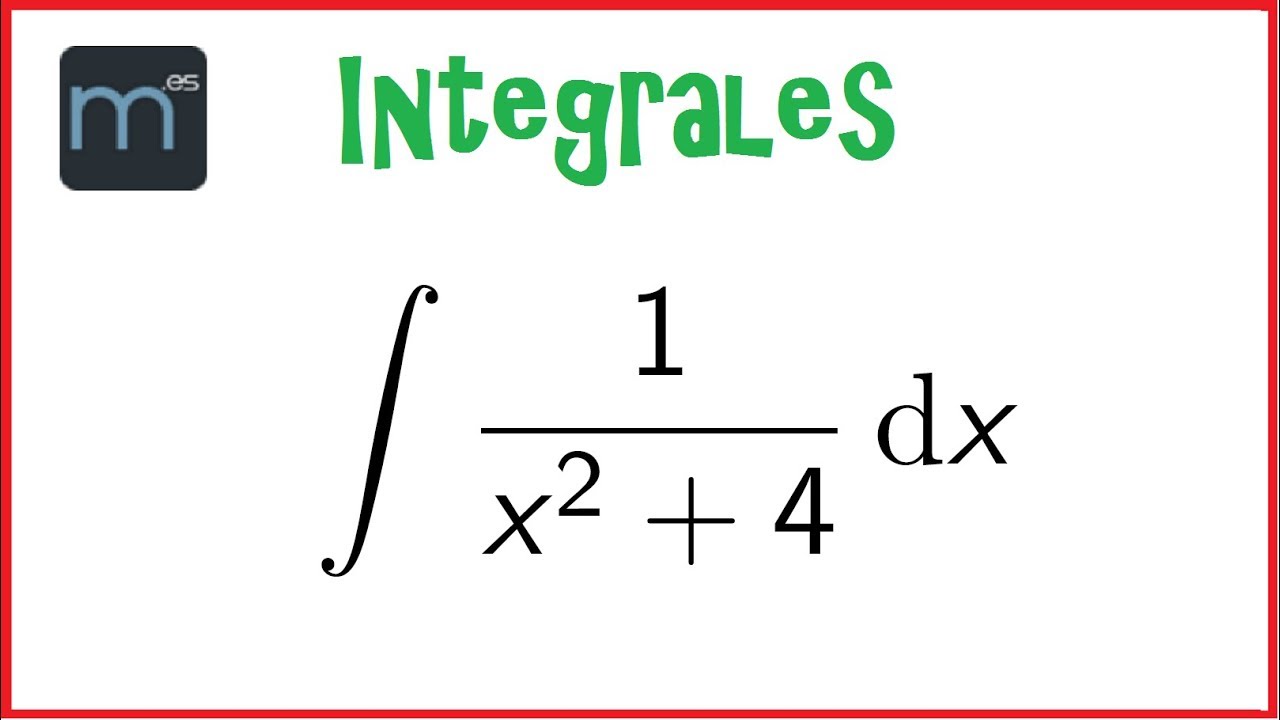¿Alguna vez te has encontrado en medio de un problema de cálculo y te has preguntado cómo se relaciona la arcotangente con la integral? Si es así, no estás solo. La arcotangente integral es un concepto fascinante y, aunque puede parecer intimidante al principio, es realmente accesible si lo desglosas. En este artículo, vamos a explorar todo lo que necesitas saber sobre la arcotangente integral, desde su definición hasta sus aplicaciones en la vida real. Así que, ¡prepárate para adentrarte en el mundo del cálculo de una manera que no habías imaginado!
¿Qué es la Arcotangente Integral?
La arcotangente integral, comúnmente denotada como ∫ (1/(1+x²)) dx, es una función que surge naturalmente en muchos problemas matemáticos y físicos. Para entenderla mejor, pensemos en la función tangente. Sabemos que la tangente es una relación de un triángulo rectángulo, pero, ¿qué pasa cuando queremos encontrar el ángulo a partir de la tangente? Aquí es donde entra en juego la arcotangente. La arcotangente nos ayuda a obtener ese ángulo, y la integral de esta función nos permite calcular el área bajo la curva de la función tangente inversa.
La Fórmula de la Arcotangente Integral
La integral de la función arcotangente se expresa como:
∫ arctan(x) dx = x arctan(x) - (1/2) ln(1+x²) + C¿Te suena complicado? No te preocupes. Vamos a desglosarlo. La integral tiene tres partes principales: el producto de x y arctan(x), un término logarítmico y la constante de integración C. Cada uno de estos componentes tiene su propia importancia y aplicabilidad. Pero, ¿cómo llegamos a esta fórmula? ¡Eso es lo que vamos a descubrir a continuación!
Derivación de la Arcotangente Integral
Para entender la derivación de la integral de la arcotangente, primero necesitamos recordar que la derivada de arctan(x) es 1/(1+x²). Esto significa que si queremos encontrar la integral, debemos pensar en la función que produce esta derivada. Al integrar, esencialmente estamos buscando la «antiderivada». Así que, si partimos de la derivada, podemos aplicar técnicas de integración por partes, que son útiles para resolver integrales que involucran productos de funciones.
Aplicaciones Prácticas de la Arcotangente Integral
Ahora que ya tenemos una idea básica de lo que es la arcotangente integral, hablemos de cómo se aplica en el mundo real. Esta función no solo es un concepto teórico; tiene aplicaciones prácticas en diversas disciplinas. Por ejemplo, en la física, se utiliza para modelar fenómenos de ondas y en la ingeniería para resolver problemas relacionados con circuitos eléctricos. ¿Te imaginas cuántas veces la arcotangente integral puede aparecer en cálculos de resistencia o en la interpretación de señales? ¡Es más común de lo que piensas!
Ejemplo de Aplicación en Física
Imagina que estás trabajando en un proyecto de física donde necesitas calcular el ángulo de un lanzamiento de proyectiles. La trayectoria de un proyectil puede describirse mediante funciones trigonométricas. Al aplicar la arcotangente integral, puedes encontrar el ángulo de lanzamiento óptimo que maximiza la distancia recorrida. Esto es solo un ejemplo de cómo esta función se convierte en una herramienta poderosa para resolver problemas prácticos.
Resolviendo Ejercicios de Arcotangente Integral
Una de las mejores maneras de dominar un concepto es a través de la práctica. Así que, ¡manos a la obra! Vamos a resolver un ejercicio típico que involucra la arcotangente integral. Supongamos que queremos calcular la integral de 1/(1+x²) desde 0 hasta 1.
Ejercicio: Calcular la Integral
La integral se establece así:
∫[0,1] (1/(1+x²)) dx
Al aplicar la arcotangente, sabemos que:
∫ (1/(1+x²)) dx = arctan(x) + CPor lo tanto, evaluamos:
arctan(1) - arctan(0) = π/4 - 0 = π/4Y ahí lo tienes, la integral de 1/(1+x²) desde 0 hasta 1 es π/4. ¡Sencillo, verdad?
Consejos para Dominar la Arcotangente Integral
Dominar la arcotangente integral requiere tiempo y práctica. Aquí hay algunos consejos que pueden ayudarte en el camino:
- Practica regularmente: La clave para mejorar en cálculo es la práctica constante. Resuelve diferentes tipos de problemas que involucren la arcotangente integral.
- Visualiza: Dibuja gráficos de la función arcotangente y su integral. Esto te ayudará a comprender cómo se comporta la función y su área bajo la curva.
- Consulta recursos: No dudes en utilizar libros de texto, videos y plataformas en línea para obtener diferentes perspectivas sobre el tema.
¿La arcotangente integral es solo una función matemática teórica?
No, tiene aplicaciones prácticas en campos como la física, la ingeniería y la estadística. Es fundamental para resolver problemas del mundo real.
¿Cómo se relaciona la arcotangente integral con otras funciones trigonométricas?
La arcotangente integral está relacionada con otras funciones trigonométricas a través de identidades y derivadas. Comprender estas relaciones puede facilitar el aprendizaje de la integral.
¿Es necesario conocer cálculo diferencial para entender la arcotangente integral?
Sí, tener una comprensión básica de cálculo diferencial te ayudará a entender mejor la derivación de la arcotangente y cómo se relaciona con su integral.
¿Dónde puedo encontrar más ejercicios sobre arcotangente integral?
Existen numerosos recursos en línea, como sitios web educativos, libros de texto y plataformas de aprendizaje que ofrecen ejercicios y problemas prácticos sobre la arcotangente integral.
¿Puedo usar la arcotangente integral en programación?
Definitivamente. Muchos lenguajes de programación tienen funciones integradas para calcular la arcotangente y sus integrales, lo que puede ser útil en simulaciones y modelados matemáticos.
En resumen, la arcotangente integral es un concepto valioso y útil que, aunque puede parecer complejo, es accesible con la práctica adecuada. A medida que sigas explorando este tema, descubrirás que no solo es una herramienta poderosa en matemáticas, sino también una puerta de entrada a una comprensión más profunda de la física y la ingeniería. Así que sigue practicando y desafiándote a ti mismo. ¡La arcotangente integral no te decepcionará!