¿Alguna vez te has preguntado cómo los matemáticos determinan los puntos más altos y bajos de una función? ¡Bienvenido al fascinante mundo de los extremos relativos! Este concepto es fundamental en el análisis de funciones y tiene aplicaciones prácticas en diversas áreas, desde la economía hasta la ingeniería. En este artículo, vamos a desglosar qué son los extremos relativos, cómo encontrarlos y por qué son importantes. Así que, si estás listo para sumergirte en este tema, ¡vamos allá!
¿Qué son los Extremos Relativos?
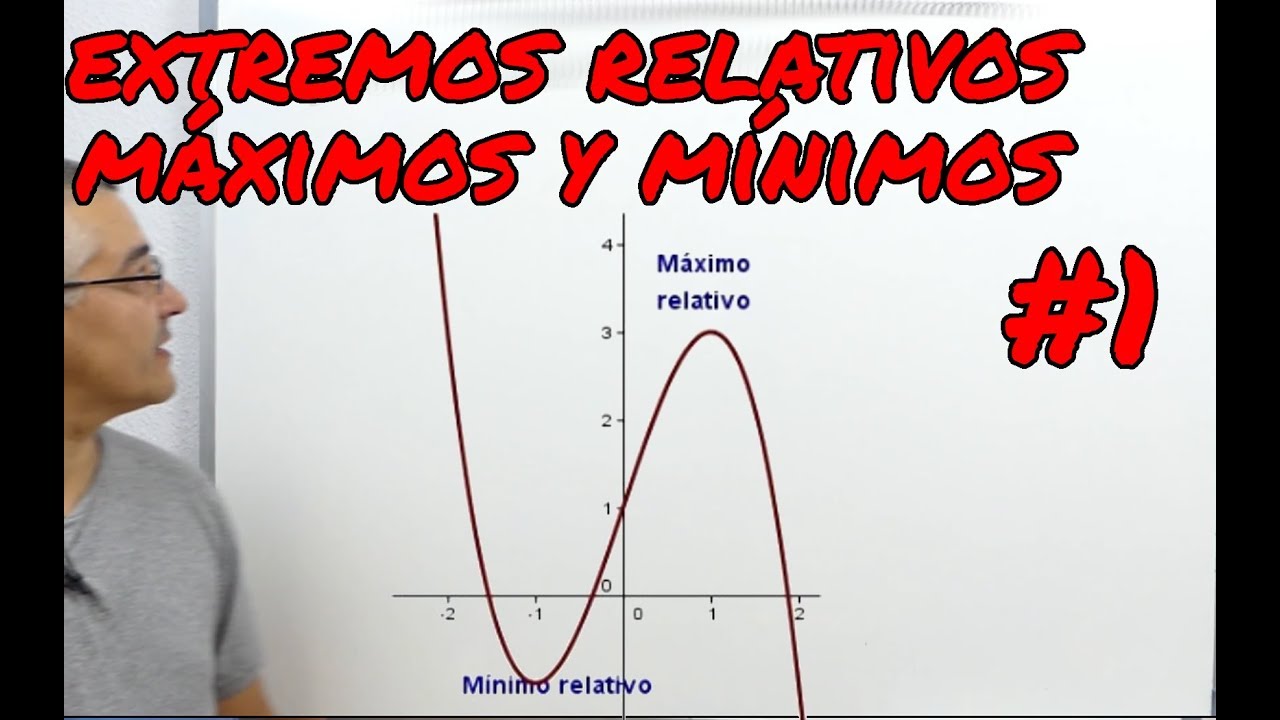
Los extremos relativos son los puntos donde una función alcanza un valor máximo o mínimo en un intervalo específico. Imagina que estás en una montaña rusa. El punto más alto que alcanzas en una subida es un máximo relativo, mientras que el punto más bajo en una bajada es un mínimo relativo. En términos matemáticos, si tienes una función f(x), un punto x0 es un máximo relativo si f(x0) es mayor que f(x) para todos los x en un intervalo alrededor de x0. De manera similar, es un mínimo relativo si f(x0) es menor que f(x) en ese mismo intervalo.
Pero, ¿por qué deberías preocuparte por los extremos relativos? En la vida real, estos puntos son cruciales. Por ejemplo, un ingeniero puede necesitar saber el punto más bajo de una estructura para asegurar su estabilidad, o un economista podría buscar el precio máximo que los consumidores están dispuestos a pagar por un producto. Los extremos relativos son, en esencia, puntos de inflexión que pueden tener un gran impacto en decisiones y resultados.
Cómo Encontrar los Extremos Relativos
Encontrar los extremos relativos puede parecer un proceso complicado, pero con un poco de práctica, se vuelve más sencillo. Aquí te dejo una guía paso a paso:
Paso 1: Derivar la Función
El primer paso para encontrar extremos relativos es calcular la derivada de la función. La derivada, en términos simples, te dice la tasa de cambio de la función en un punto dado. Si la derivada es positiva, la función está aumentando; si es negativa, está disminuyendo. Cuando la derivada es cero, es posible que estés en un extremo relativo.
Paso 2: Igualar la Derivada a Cero
Una vez que tienes la derivada, iguala la ecuación a cero y resuelve para x. Esto te dará los puntos críticos, que son candidatos a extremos relativos. Recuerda que no todos los puntos críticos son extremos, así que sigue leyendo.
Paso 3: Prueba de la Segunda Derivada
Aquí es donde se pone interesante. Para determinar si un punto crítico es un máximo o un mínimo relativo, necesitas calcular la segunda derivada de la función. Si la segunda derivada en ese punto es positiva, entonces tienes un mínimo relativo. Si es negativa, tienes un máximo relativo. Si es cero, necesitarás hacer más análisis.
Paso 4: Análisis de los Límites
Finalmente, no olvides considerar los límites de la función. A veces, los extremos pueden ocurrir en los bordes del intervalo que estás analizando. Así que asegúrate de evaluar la función en esos puntos también.
Ejemplo Práctico
Para ilustrar estos pasos, veamos un ejemplo práctico. Supongamos que tienes la función f(x) = -x² + 4x. Vamos a encontrar sus extremos relativos.
Derivada de la Función
Primero, derivamos la función:
f'(x) = -2x + 4.
Igualando a Cero
Ahora igualamos la derivada a cero:
-2x + 4 = 0 → x = 2.
Este es nuestro punto crítico. Ahora vamos a determinar si es un máximo o un mínimo.
Segunda Derivada
Calculamos la segunda derivada:
f»(x) = -2.
Como la segunda derivada es negativa, sabemos que x = 2 es un máximo relativo. Ahora, evaluamos la función en este punto:
f(2) = -(2)² + 4(2) = 8.
Así que, tenemos un máximo relativo en (2, 8).
Importancia de los Extremos Relativos
Ahora que sabes cómo encontrarlos, es importante entender su relevancia. Los extremos relativos son útiles en muchos campos. Por ejemplo, en la economía, se utilizan para maximizar ganancias o minimizar costos. En la biología, pueden ayudar a modelar el crecimiento de poblaciones. En el diseño gráfico, los extremos pueden ayudar a determinar las proporciones estéticas de un diseño.
Además, los extremos relativos también son cruciales en la optimización. Cuando necesitas encontrar la mejor solución a un problema, identificar estos puntos puede guiarte hacia la respuesta correcta. Así que, ya sea que estés estudiando matemáticas o aplicando estos conceptos en tu vida diaria, los extremos relativos son una herramienta poderosa.
¿Los extremos relativos siempre son máximos o mínimos absolutos?
No, los extremos relativos son específicos a un intervalo. Un extremo relativo puede no ser el máximo o mínimo absoluto de toda la función.
¿Qué pasa si la derivada nunca es cero?
Si la derivada no tiene puntos donde sea cero, eso significa que la función es monótona (siempre creciente o siempre decreciente) en ese intervalo y no tiene extremos relativos.
¿Se pueden encontrar extremos relativos en funciones no derivables?
En general, para encontrar extremos relativos, necesitas que la función sea derivable. Sin embargo, hay métodos para identificar extremos en funciones que tienen puntos de no derivabilidad, pero son más complicados.
¿Qué papel juegan los extremos relativos en el cálculo integral?
Los extremos relativos son importantes en el cálculo integral porque pueden ayudarte a determinar áreas bajo la curva y optimizar funciones en problemas de maximización o minimización.
¿Existen técnicas gráficas para encontrar extremos relativos?
Sí, graficar la función puede ser muy útil. A menudo, puedes visualizar los extremos relativos observando dónde la curva cambia de dirección.
Con todo esto, ahora tienes una comprensión sólida de los extremos relativos. Ya sea que estés estudiando para un examen o simplemente tengas curiosidad, espero que este artículo te haya proporcionado información valiosa y fácil de entender. ¡Sigue explorando el maravilloso mundo de las matemáticas!