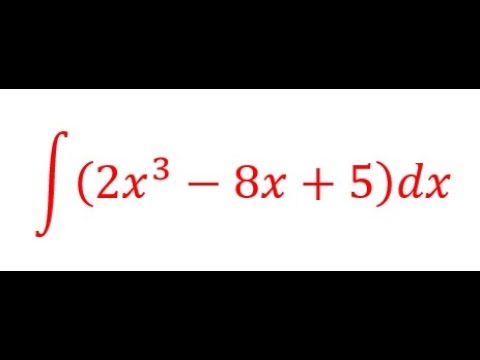Ejercicios de Integrales Indefinidas: Guía Completa para Practicar y Dominar

Las integrales indefinidas son uno de esos conceptos en cálculo que, al principio, pueden parecer un verdadero rompecabezas. Pero, ¿sabías que, una vez que entiendes los fundamentos, se convierten en una herramienta poderosa en tu arsenal matemático? En este artículo, vamos a desglosar las integrales indefinidas, ofreciéndote una guía completa que te permitirá practicar y dominar este tema. Desde los conceptos básicos hasta ejercicios más avanzados, aquí encontrarás todo lo que necesitas para convertirte en un experto en integrales. Así que, si estás listo para sumergirte en el mundo de las matemáticas, ¡comencemos!

¿Qué son las Integrales Indefinidas?

Primero, pongamos las cartas sobre la mesa. ¿Qué es una integral indefinida? En términos simples, una integral indefinida es una forma de encontrar la función original a partir de su derivada. Es como si estuvieras retrocediendo en el tiempo para descubrir de dónde vino una función. Matemáticamente, se expresa como:

∫f(x)dx = F(x) + C

Donde F(x) es la función primitiva de f(x) y C es la constante de integración. La constante es crucial, porque al derivar una constante, se «pierde» en el proceso, así que siempre la incluimos para mantener todas las posibles funciones originales.

¿Por qué son importantes las Integrales Indefinidas?

Imagina que estás navegando por un río. Las integrales indefinidas son como un mapa que te ayuda a entender el flujo del agua. Te permiten calcular áreas bajo curvas, resolver problemas de física, y modelar situaciones en la vida real, como el crecimiento poblacional o la acumulación de recursos. Así que, si piensas que las integrales son solo un capricho académico, ¡piénsalo de nuevo! Son herramientas prácticas que tienen aplicaciones en diversas disciplinas.

Reglas Básicas de Integración

Antes de lanzarnos a los ejercicios, hablemos de algunas reglas básicas que necesitas conocer. Estas son como las recetas que seguirás en la cocina de las matemáticas:

• Constantes: ∫a dx = ax + C, donde a es una constante.
• Poder: ∫x^n dx = (x^(n+1))/(n+1) + C, para n ≠ -1.
• Exponencial: ∫e^x dx = e^x + C.
• Trigonométricas: ∫sin(x) dx = -cos(x) + C y ∫cos(x) dx = sin(x) + C.

Estas reglas son tus aliadas. Familiarízate con ellas, porque te ayudarán a resolver muchos ejercicios de manera más rápida y eficiente.

Ejercicios Prácticos de Integrales Indefinidas

Ahora que tenemos las bases cubiertas, es hora de practicar. Aquí te dejo algunos ejercicios que van desde lo básico hasta lo más avanzado. ¡No te asustes! Recuerda, cada paso cuenta.

Ejercicio 1: Integrar una Constante

Vamos a empezar con algo sencillo. Integra la constante 5:

∫5 dx

Siguiendo la regla de las constantes, sabemos que:

∫5 dx = 5x + C

¡Fácil, verdad? Ahora, intenta resolverlo tú mismo con diferentes constantes. ¿Qué pasa si cambias el 5 por un 10 o un -3? ¿Ves cómo el proceso sigue siendo el mismo?

Ejercicio 2: Potencias de x

Pasemos a algo un poco más complicado. Integra la función x^3:

∫x^3 dx

Usando la regla de potencias, tenemos:

∫x^3 dx = (x^(3+1))/(3+1) + C = (x^4)/4 + C

Intenta resolverlo con diferentes exponentes. ¿Cómo se siente al ver que el patrón se repite?

Ejercicio 3: Funciones Exponenciales

Ahora, integremos una función exponencial. ¿Qué tal si integramos e^(2x)?

∫e^(2x) dx

Para esto, recuerda que al integrar e^(ax), donde a es una constante, el resultado es:

(1/a)e^(ax) + C

Así que, aplicando esto:

∫e^(2x) dx = (1/2)e^(2x) + C

Integración por Sustitución

¿Te has dado cuenta de que a veces las funciones pueden parecer un poco enredadas? Aquí es donde la técnica de sustitución entra en juego. Es como cambiar un rompecabezas complicado por uno más sencillo.

Ejemplo de Sustitución

Considera la integral:

∫(3x^2)(e^(x^3)) dx

Podemos hacer una sustitución donde u = x^3. Entonces, du = 3x^2 dx. Así que podemos reescribir nuestra integral como:

∫e^u du = e^u + C = e^(x^3) + C

¡Y voilà! Has simplificado una integral que parecía compleja. Intenta aplicar esta técnica en otros ejercicios y observa cómo te ayuda a deshacerte de las complicaciones.

Integrales Indefinidas con Funciones Trigonométricas

Las funciones trigonométricas pueden ser un poco traviesas, pero no te preocupes, ¡tenemos las herramientas necesarias para manejarlas!

Ejercicio de Seno y Coseno

Integra la función seno:

∫sin(x) dx

Recuerda que:

∫sin(x) dx = -cos(x) + C

Ahora, ¿qué tal si intentas con coseno? ¿Ves cómo las funciones trigonométricas tienen patrones similares?

Consejos para Dominar las Integrales Indefinidas

Ahora que has practicado algunos ejercicios, aquí hay algunos consejos que pueden ayudarte a dominar las integrales indefinidas:

• Practica Regularmente: La práctica hace al maestro. Dedica un tiempo cada semana a resolver integrales.
• Revisa los Errores: Cuando cometas un error, revisa qué salió mal. Aprender de tus errores es crucial.
• Utiliza Recursos: Hay muchos recursos en línea, desde videos hasta foros de discusión. No dudes en utilizarlos.

¿Qué es la constante de integración y por qué es importante?

La constante de integración es esencial porque representa todas las posibles funciones que podrían derivarse de la función que estás integrando. Sin ella, perderías información importante.

¿Cómo puedo saber qué técnica de integración usar?

Con la práctica, comenzarás a reconocer patrones en las funciones que te ayudarán a decidir qué técnica usar. La sustitución es útil para funciones compuestas, mientras que la integración por partes es mejor para productos de funciones.

¿Puedo usar una calculadora para resolver integrales indefinidas?

¡Claro! Las calculadoras pueden ser herramientas útiles para verificar tus respuestas. Sin embargo, es fundamental entender el proceso detrás de la integral para poder resolver problemas más complejos en el futuro.

En resumen, las integrales indefinidas son un tema fascinante y esencial en matemáticas. Con práctica y dedicación, puedes dominarlas y aplicarlas en diversos contextos. Así que, ¡sigue practicando y no te rindas!