¡Hola! Hoy vamos a sumergirnos en el fascinante mundo de los números y, más específicamente, en el Algoritmo de Euclides. ¿Alguna vez te has preguntado cómo se pueden encontrar los números que son comunes entre varios? O, en otras palabras, ¿cómo se calcula el Máximo Común Divisor (MCD)? Este concepto puede parecer complicado al principio, pero no te preocupes, estoy aquí para guiarte a través de cada paso. Imagina que el MCD es como el mejor amigo que comparten dos números: es el mayor número que puede dividir a ambos sin dejar un residuo. ¿Listo para descubrirlo? ¡Vamos a ello!
¿Qué es el Máximo Común Divisor (MCD)?
Primero, aclaremos qué es exactamente el MCD. El Máximo Común Divisor es el número más grande que divide exactamente a dos o más números. Por ejemplo, si tomamos los números 12 y 15, el MCD sería 3, ya que es el número más grande que puede dividir ambos sin dejar un residuo. Pero, ¿cómo llegamos a ese número? Aquí es donde entra en juego el Algoritmo de Euclides, un método antiguo pero eficaz que nos ayuda a calcular el MCD de manera rápida y sencilla.
El Algoritmo de Euclides: Un Método Clásico
El Algoritmo de Euclides se basa en una idea simple: si tienes dos números, puedes encontrar su MCD utilizando el residuo de su división. ¡Es como un juego de eliminación! Comenzamos dividiendo el número más grande por el más pequeño y, en lugar de quedarnos con el cociente, nos enfocamos en el residuo. Luego repetimos este proceso: tomamos el divisor anterior y el residuo y los dividimos nuevamente. ¿Suena complicado? ¡No te preocupes! Vamos a desglosarlo.
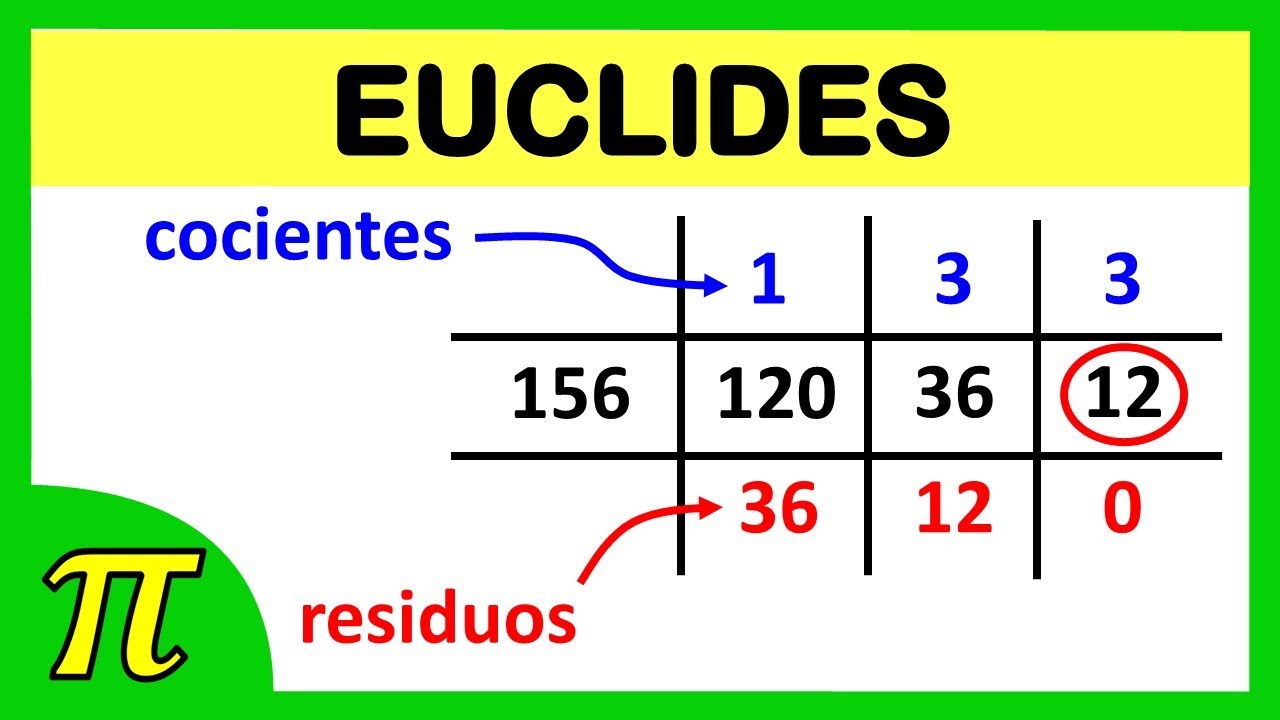
Ejemplo Paso a Paso del Algoritmo de Euclides
Imaginemos que queremos encontrar el MCD de 48 y 18. Empezamos dividiendo 48 entre 18. El cociente es 2 y el residuo es 12. Ahora, en lugar de seguir con 48, tomamos 18 y 12. Así que, la próxima división es 18 dividido por 12, lo que nos da un cociente de 1 y un residuo de 6. Continuamos con 12 y 6, y encontramos que 12 dividido por 6 da un residuo de 0. ¡Y ahí lo tenemos! Cuando el residuo es 0, el divisor en la última división no nula (en este caso, 6) es el MCD. Así que el MCD de 48 y 18 es 6.
Por Qué Usar el Algoritmo de Euclides
Ahora que hemos pasado por un ejemplo práctico, quizás te estés preguntando: “¿Por qué debería preocuparme por aprender este método?” Bueno, el Algoritmo de Euclides es increíblemente eficiente, especialmente cuando trabajamos con números grandes. A diferencia de otros métodos que requieren descomposición en factores primos, el Algoritmo de Euclides se basa en divisiones sucesivas, lo que lo hace mucho más rápido. Es como hacer una carrera: a veces, la ruta más corta no es la más obvia.
Aplicaciones del MCD en la Vida Real
Quizás te estés preguntando cómo se aplica el MCD en la vida real. Imagina que estás organizando una fiesta y quieres repartir bocadillos de manera equitativa entre tus amigos. Si tienes 24 galletas y 36 mini pizzas, el MCD te ayudará a determinar cuántos grupos de amigos puedes formar sin que sobre nada. Usando el MCD, descubrirás que puedes formar 12 grupos, asegurando que todos reciban la misma cantidad de bocadillos. Así que, ¡gracias al MCD, tu fiesta será un éxito!
Variaciones del Algoritmo de Euclides
El Algoritmo de Euclides tiene varias versiones. Por ejemplo, existe una versión llamada «Algoritmo de Euclides extendido», que no solo encuentra el MCD, sino que también proporciona coeficientes que permiten expresar el MCD como una combinación lineal de los dos números originales. Esto es útil en teoría de números y criptografía. ¡Es como un truco extra que te da más información de la que esperabas!
Implementación del Algoritmo de Euclides en Programación
Si te gusta la programación, implementar el Algoritmo de Euclides es un ejercicio muy práctico. Puedes usarlo en casi cualquier lenguaje de programación. Aquí tienes un pequeño ejemplo en Python:
def mcd(a, b):
while b != 0:
a, b = b, a % b
return a
print(mcd(48, 18)) # Salida: 6
Como puedes ver, es muy sencillo. Solo necesitas un bucle que siga dividiendo hasta que el residuo sea 0. ¡Así de fácil!
Consejos para Practicar el MCD
Si quieres volverte un experto en encontrar el MCD, aquí hay algunos consejos prácticos:
- Practica con números pequeños: Comienza con números sencillos para entender el proceso antes de avanzar a números más grandes.
- Hazlo a mano: Aunque es tentador usar una calculadora, practicar a mano te ayudará a comprender mejor el algoritmo.
- Utiliza problemas de la vida real: Encuentra situaciones en tu vida diaria donde necesites calcular el MCD. Esto hará que el aprendizaje sea más significativo.
¿El MCD siempre es un número positivo?
Sí, el MCD siempre es un número positivo, ya que estamos hablando de divisores. Sin embargo, el MCD de un número y 0 es el propio número.
¿Puedo usar el Algoritmo de Euclides para más de dos números?
¡Absolutamente! Puedes encontrar el MCD de más de dos números aplicando el algoritmo de manera sucesiva. Por ejemplo, para encontrar el MCD de 48, 18 y 30, primero calcula el MCD de 48 y 18, y luego usa ese resultado para calcular el MCD con 30.
¿Qué pasa si uno de los números es negativo?
El MCD se define solo para números enteros positivos, así que si tienes un número negativo, simplemente ignora el signo y calcula el MCD con su valor absoluto.
¿Es el MCD lo mismo que el mínimo común múltiplo (MCM)?
No, el MCD y el MCM son conceptos diferentes. Mientras que el MCD se refiere al número más grande que puede dividir a dos o más números, el MCM se refiere al número más pequeño que es múltiplo de esos números.
¿Cómo puedo mejorar mi velocidad en el cálculo del MCD?
La práctica es clave. Cuanto más familiarizado estés con el algoritmo, más rápido podrás calcular el MCD. También puedes intentar memorizar algunos MCD comunes para agilizar el proceso.
Y ahí lo tienes, un recorrido completo por el Algoritmo de Euclides y el MCD. Espero que ahora tengas una mejor comprensión de este concepto y te sientas preparado para aplicarlo en tu vida diaria. ¡No dudes en practicar y hacer preguntas si algo no queda claro!