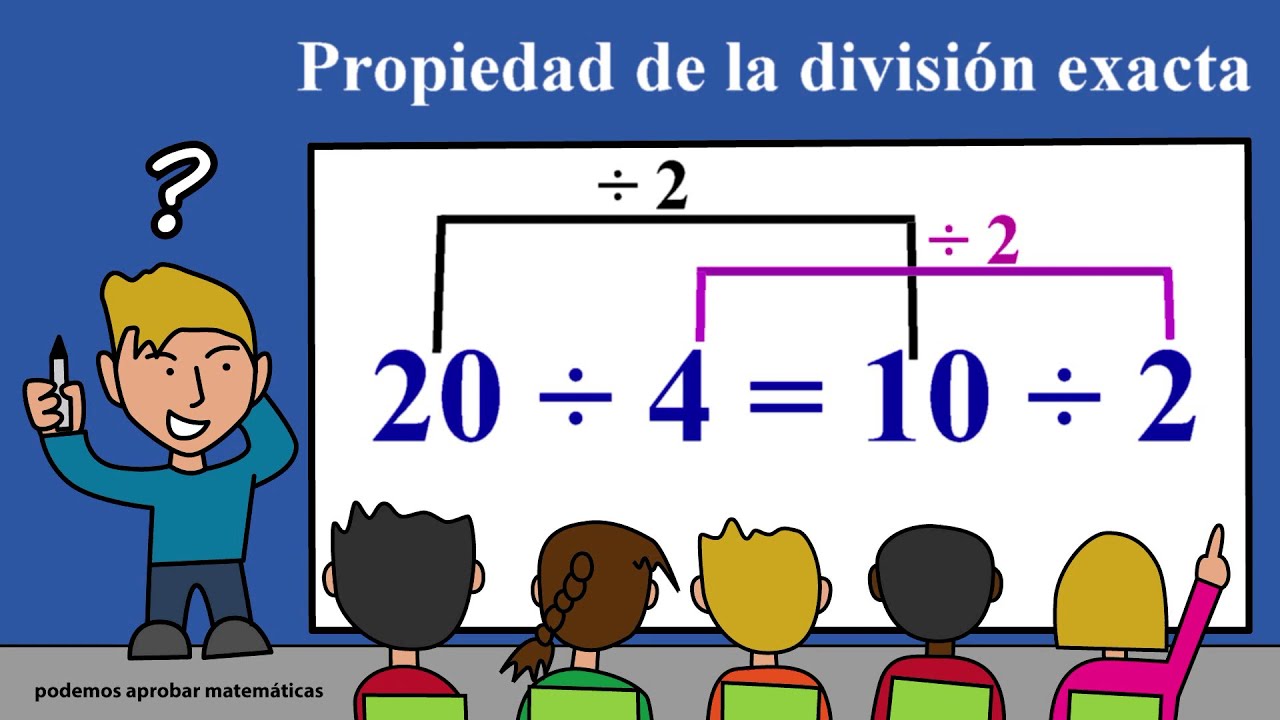
La matemática puede parecer, en ocasiones, un laberinto enredado de números y símbolos. Pero, ¿y si te dijera que entender ciertos conceptos puede ser tan sencillo como seguir un mapa claro? Uno de esos conceptos es la propiedad de la división exacta, que, aunque suena complicada, es bastante intuitiva. En este artículo, vamos a desglosar este tema, paso a paso, para que puedas dominarlo sin problemas. Así que, si alguna vez te has sentido perdido en la jungla de las divisiones, ¡este es tu momento de brillar!
La división exacta es una herramienta poderosa en el mundo de las matemáticas. Se refiere a la situación en la que un número se puede dividir por otro sin dejar un residuo. Por ejemplo, si tomamos 10 y lo dividimos por 2, el resultado es 5. Pero si intentamos dividir 10 por 3, el resultado es 3, con un residuo de 1. La división exacta nos dice que 10 no es divisible por 3 de manera exacta, lo que es un concepto fundamental que puede aplicarse en diversos contextos, desde la aritmética básica hasta la teoría de números más avanzada.
¿Qué es la División Exacta?
La división exacta, en términos simples, ocurre cuando un número (llamado dividendo) puede ser dividido por otro número (llamado divisor) y el resultado es un número entero. Imagina que tienes un pastel y decides compartirlo con tus amigos. Si el pastel se puede dividir perfectamente entre todos, ¡eso es una división exacta! Pero si sobran migajas, entonces no lo es. Así que, en matemáticas, buscamos esos casos donde todo se reparte de manera justa y equitativa.
Ejemplos Prácticos de División Exacta
Para que este concepto sea aún más claro, veamos algunos ejemplos. Supongamos que tienes 12 galletas y quieres repartirlas entre 4 amigos. ¿Cuántas galletas recibe cada uno? Si haces la división 12 ÷ 4, obtienes 3. No hay galletas sobrantes, lo que significa que 12 es divisible por 4 de manera exacta. Ahora, si intentamos dividir esas mismas 12 galletas entre 5 amigos, obtendremos 2 galletas para cada uno, pero sobraría 2 galletas. En este caso, 12 no es divisible por 5 de forma exacta.
Propiedades de la División Exacta
Ahora que tenemos una comprensión básica de lo que es la división exacta, hablemos de algunas propiedades que la rodean. Esto no solo hará que el concepto sea más claro, sino que también te ayudará a aplicar estas propiedades en diferentes problemas matemáticos.
La Propiedad de la Divisibilidad
La propiedad de la divisibilidad es el principio que establece que si un número A se puede dividir por un número B sin dejar un residuo, decimos que A es divisible por B. Por ejemplo, 20 es divisible por 5, ya que 20 ÷ 5 = 4, sin residuo. Este concepto es fundamental para entender la división exacta, ya que nos ayuda a identificar qué números son divisores de otros.
Múltiplos y Divisores
Para entender la división exacta, es crucial conocer la relación entre múltiplos y divisores. Un número A es múltiplo de B si puedes obtener A al multiplicar B por un número entero. Por ejemplo, 15 es un múltiplo de 3 porque 3 × 5 = 15. En cambio, 3 es un divisor de 15, ya que 15 ÷ 3 = 5. Esta relación es esencial al estudiar la división exacta.
Aplicaciones de la División Exacta
La división exacta no es solo un concepto teórico; tiene aplicaciones prácticas en la vida cotidiana. Desde la distribución de recursos hasta la planificación de eventos, entender cómo funciona puede facilitar muchas tareas.
Distribución de Recursos
Imagina que estás organizando una fiesta y necesitas comprar refrescos. Si tienes 24 latas y decides que cada invitado debe recibir 4 latas, puedes dividir 24 ÷ 4, y el resultado es 6. Esto significa que puedes invitar a 6 amigos sin que sobre ninguna lata. Aquí, la división exacta te ayuda a planificar de manera efectiva.
Resolución de Problemas Matemáticos
En el ámbito académico, la división exacta es fundamental para resolver problemas de matemáticas. Por ejemplo, si estás trabajando con fracciones y necesitas simplificarlas, entender la división exacta te permitirá encontrar el máximo común divisor, lo que es esencial para simplificar las fracciones correctamente.
Errores Comunes en la División Exacta
Como en cualquier área del conocimiento, es fácil caer en errores al trabajar con la división exacta. Aquí te dejamos algunos de los más comunes y cómo evitarlos.
No Verificar el Residuo
Uno de los errores más comunes es no verificar si hay un residuo después de realizar una división. Siempre que dividas dos números, asegúrate de comprobar si el resultado es un número entero o si hay un residuo. Esto es clave para determinar si la división es exacta o no.
Confundir Divisores y Múltiplos
Otro error frecuente es confundir los conceptos de múltiplos y divisores. Recuerda que un divisor es un número que divide a otro sin dejar residuo, mientras que un múltiplo es el resultado de multiplicar un número por un entero. Mantener claros estos conceptos te ayudará a evitar confusiones.
Ejercicios Prácticos para Mejorar tu Comprensión
La mejor manera de aprender sobre la división exacta es practicar. Aquí tienes algunos ejercicios que puedes intentar.
Ejercicio 1
Determina si los siguientes números son divisibles entre 3: 27, 34, 45, 51. ¿Cuáles son divisibles y cuáles no?
Ejercicio 2
Si tienes 60 caramelos y quieres repartirlos entre 8 niños, ¿cuántos caramelos recibe cada niño y cuántos sobran?
Ejercicio 3
Encuentra todos los divisores de 36. ¿Cuántos son y cuáles son?
La propiedad de la división exacta es un concepto fundamental en matemáticas que nos ayuda a entender cómo los números se relacionan entre sí. A través de ejemplos prácticos y ejercicios, puedes dominar este concepto y aplicarlo en diversas situaciones cotidianas. Recuerda que la práctica es clave para reforzar tu comprensión y mejorar tus habilidades matemáticas.
¿Qué es la división exacta?
La división exacta ocurre cuando un número se puede dividir por otro sin dejar un residuo, resultando en un número entero.
¿Cómo puedo saber si un número es divisible por otro?
Puedes comprobar si un número es divisible por otro realizando la división y verificando si el resultado es un número entero, sin residuo.
¿Por qué es importante la división exacta en la vida diaria?
La división exacta se utiliza en situaciones cotidianas como la distribución de recursos, la planificación de eventos y la resolución de problemas matemáticos.
¿Cuáles son algunos errores comunes al trabajar con la división exacta?
Los errores comunes incluyen no verificar el residuo después de una división y confundir divisores y múltiplos.
¿Cómo puedo mejorar mi comprensión de la división exacta?
La práctica es clave. Intenta resolver ejercicios relacionados con la división exacta y verifica tus respuestas para aprender de tus errores.