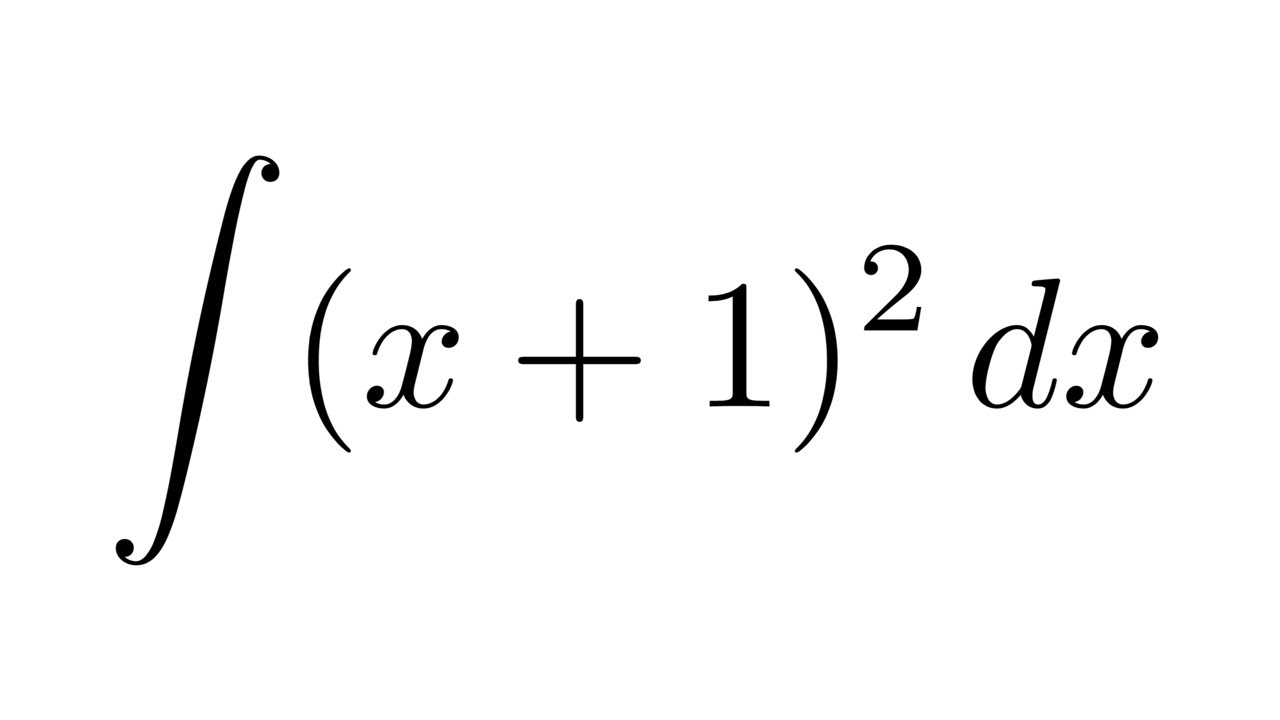¿Alguna vez te has encontrado mirando una integral y te has preguntado cómo demonios se hace? No te preocupes, porque hoy vamos a desglosar el proceso de calcular la integral de x^1/2, que también se conoce como la raíz cuadrada de x. Este es un tema fundamental en cálculo, y aunque puede parecer intimidante al principio, lo vamos a hacer sencillo y comprensible. Así que, ponte cómodo y prepárate para sumergirte en el fascinante mundo de las integrales.
La integral de x^1/2 es una de esas que aparecen con frecuencia en problemas de matemáticas y física, y entender cómo resolverla te abrirá las puertas a muchos otros conceptos. Antes de entrar en materia, aclaremos algunos términos. La integral, en esencia, es una forma de sumar áreas bajo curvas. Así que, al calcular la integral de x^1/2, estamos buscando el área bajo la curva de la función y, créeme, es más fácil de lo que parece. ¡Vamos a ello!
Entendiendo la Integral Indefinida
Primero, hablemos de lo que es una integral indefinida. Este tipo de integral nos da una función antiderivada más una constante. Es como si estuvieras buscando un mapa que te lleve a un destino, pero en lugar de un lugar físico, buscas una función matemática. En nuestro caso, queremos encontrar la función cuya derivada es x^1/2.
La notación que utilizamos para la integral indefinida es la siguiente:
∫ x^(1/2) dx
Así que, en este caso, estamos buscando la antiderivada de x^(1/2). Ahora, hay una regla que nos ayuda aquí: la regla de potencia. Esta regla dice que si tienes una función en la forma x^n, la integral se puede calcular como:
∫ x^n dx = (x^(n+1))/(n+1) + C
donde C es la constante de integración. Esto es como una receta de cocina: necesitas los ingredientes correctos y seguir los pasos adecuados para obtener el resultado deseado.
Aplicando la Regla de Potencia
Ahora que tenemos la regla, vamos a aplicarla a nuestra integral. En este caso, n es igual a 1/2. Así que, siguiendo la regla de potencia, tenemos:
∫ x^(1/2) dx = (x^(1/2 + 1))/(1/2 + 1) + C
Simplificando eso, obtenemos:
∫ x^(1/2) dx = (x^(3/2))/(3/2) + C
Recuerda que cuando dividimos por una fracción, es lo mismo que multiplicar por su recíproco. Así que podemos reescribirlo como:
∫ x^(1/2) dx = (2/3) x^(3/2) + C
¡Y ahí lo tenemos! Hemos encontrado la integral de x^1/2. Pero, espera, aún hay más que explorar. Vamos a profundizar un poco más en el tema.
Interpretando el Resultado
Ahora que tenemos la integral, es importante entender qué significa. La expresión (2/3) x^(3/2) + C representa un conjunto de funciones. Cada valor de C te dará una función diferente, pero todas comparten la misma forma general. Esto es como tener un grupo de amigos que se parecen entre sí, pero cada uno tiene su propia personalidad.
Por ejemplo, si C es 0, tendrías (2/3) x^(3/2). Pero si C es 5, tendrías (2/3) x^(3/2) + 5. Ambos son funciones válidas, pero cada una representa una línea diferente en el gráfico. Al sumar la constante C, estamos considerando todas las posibles funciones que pueden derivar a x^(1/2).
Gráficos y Visualización
Entender las integrales también implica visualizar lo que estamos haciendo. Imagina que trazamos la función x^1/2 en un gráfico. Esta curva empieza en el origen (0,0) y se eleva hacia la derecha, mostrando cómo la raíz cuadrada crece a medida que x aumenta. Ahora, al calcular la integral, estamos determinando el área bajo esta curva desde un punto hasta otro.
Si dibujas la gráfica de la función (2/3) x^(3/2), notarás que también se eleva, pero a un ritmo diferente. La integral no solo nos da una función; nos da una nueva perspectiva sobre cómo se relacionan las áreas y las funciones.
Ejemplo Práctico
Para solidificar tu comprensión, veamos un ejemplo práctico. Supongamos que queremos calcular la integral de x^1/2 desde 0 hasta 4. Esto se conoce como una integral definida, y se expresa así:
∫[0, 4] x^(1/2) dx
Usamos nuestra antiderivada (2/3) x^(3/2) y evaluamos desde 0 hasta 4:
(2/3) [4^(3/2) – 0^(3/2)]
Calculando esto, primero encontramos 4^(3/2), que es igual a 8. Así que ahora tenemos:
(2/3) [8 – 0] = (2/3) * 8 = 16/3
¡Y ahí tienes! El área bajo la curva de x^1/2 desde 0 hasta 4 es 16/3. Esto es como calcular cuánta pintura necesitas para cubrir una pared: estás midiendo el espacio bajo la curva.
Aspectos Avanzados: Integrales Definidas y Teorema Fundamental del Cálculo
Ya hemos hablado sobre integrales indefinidas y definidas, pero hay un aspecto crucial que no podemos dejar de lado: el Teorema Fundamental del Cálculo. Este teorema conecta las derivadas y las integrales de una manera profunda. En términos simples, nos dice que si tienes una función continua, puedes usar la integral definida para encontrar el área bajo la curva de esa función.
La belleza de este teorema radica en que nos permite calcular áreas de manera eficiente. En lugar de tener que sumar infinitos rectángulos bajo la curva, podemos usar la antiderivada para obtener el resultado en un solo paso.
Ejercicios para Practicar
Ahora que hemos cubierto los conceptos básicos y algunos ejemplos, es hora de poner en práctica lo que has aprendido. Aquí hay algunos ejercicios que puedes intentar:
1. Calcula la integral de x^1/2 desde 1 hasta 9.
2. Encuentra la integral indefinida de x^(1/2) + x^(1/3).
3. Evalúa la integral definida de x^1/2 desde 0 hasta 1.
Recuerda que la práctica es clave. Cuanto más trabajes con estas integrales, más cómodo te sentirás.
En resumen, calcular la integral de x^1/2 no es tan complicado como parece. Con un poco de práctica y entendimiento de las reglas básicas, puedes abordar este tipo de problemas con confianza. Recuerda que las integrales son una herramienta poderosa en matemáticas, y dominar su cálculo te permitirá resolver problemas más complejos en el futuro.
Así que la próxima vez que te enfrentes a una integral, recuerda nuestra guía y los pasos que hemos seguido. ¿Te sientes listo para afrontar nuevos desafíos matemáticos? ¿Qué otros temas te gustaría explorar en el mundo de las integrales?
¿Por qué es importante aprender sobre integrales?
Las integrales son fundamentales en muchas áreas de las matemáticas y la física. Te permiten calcular áreas, volúmenes y resolver problemas de movimiento, entre otros.
¿Cómo puedo mejorar mis habilidades en cálculo?
La práctica es esencial. Intenta resolver diferentes tipos de integrales y busca recursos en línea o libros de texto que te ofrezcan problemas desafiantes.
¿Qué debo hacer si me siento atascado en un problema de integral?
No dudes en pedir ayuda. Puedes consultar a un profesor, un compañero de clase o buscar tutoriales en línea. A veces, un nuevo enfoque puede hacer toda la diferencia.
¿Es necesario conocer derivadas para entender integrales?
Sí, las derivadas y las integrales están íntimamente relacionadas. Comprender cómo funcionan las derivadas te ayudará a entender mejor las integrales.
¿Las integrales tienen aplicaciones en la vida real?
Absolutamente. Las integrales se utilizan en ingeniería, economía, biología y muchas otras disciplinas para modelar y resolver problemas del mundo real.