El plano lineal es un concepto que puede sonar un poco intimidante al principio, pero en realidad es bastante sencillo una vez que lo desglosamos. Imagina que estás dibujando en una hoja de papel. Cada línea que trazas representa una relación entre dos variables. En términos más técnicos, un plano lineal es una representación gráfica de una ecuación lineal, que describe cómo una variable depende de otra. Así que, si alguna vez te has preguntado cómo se relacionan dos cosas en el mundo real, ¡estás en el lugar correcto! A lo largo de este artículo, exploraremos en profundidad qué es un plano lineal, cómo se utiliza y algunos ejemplos prácticos que te ayudarán a comprenderlo mejor.
Vamos a sumergirnos en este fascinante tema. ¿Te has dado cuenta de que en la vida diaria, muchas cosas pueden ser representadas por líneas rectas? Desde la economía hasta la biología, el plano lineal se presenta en múltiples disciplinas. Pero, ¿qué lo hace tan especial? La respuesta radica en su simplicidad y versatilidad. ¿Te gustaría saber más sobre cómo funciona? ¡Sigue leyendo!
¿Qué es un Plano Lineal?
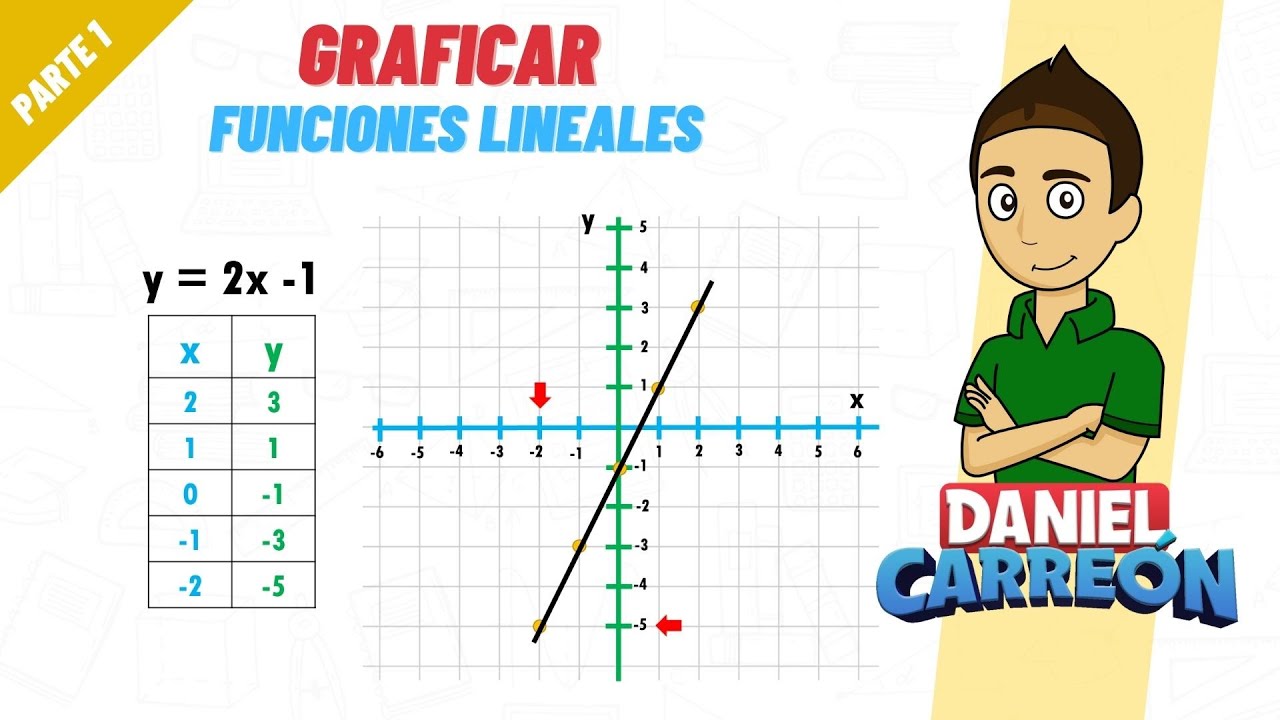
Un plano lineal, en términos matemáticos, se refiere a un espacio bidimensional que puede ser representado por una ecuación lineal de la forma y = mx + b. Aquí, «m» representa la pendiente de la línea, que indica la inclinación, y «b» es la intersección en el eje y, es decir, el punto donde la línea cruza el eje vertical. ¿Te imaginas una montaña? La pendiente te diría qué tan empinada es esa montaña, mientras que la intersección en el eje y te indicaría desde dónde comenzamos a escalar.
Este concepto no solo es fundamental en matemáticas, sino que también se aplica en diversas áreas como la física, la economía y la estadística. Por ejemplo, en economía, podrías usar un plano lineal para mostrar la relación entre el precio de un producto y la cantidad demandada. Así que, cada vez que veas una gráfica que parezca una línea recta, piensa en el plano lineal y en cómo simplifica la comprensión de las relaciones entre variables.
Ejemplos Prácticos de Planos Lineales
Ejemplo 1: Relación entre Precio y Cantidad Demandada
Imagina que eres el dueño de una pequeña tienda de café. Sabes que cuando el precio de una taza de café es bajo, más personas vienen a comprar. Si trazas esta relación en un gráfico, verás que a medida que el precio disminuye, la cantidad demandada aumenta. Esta es una representación clásica de un plano lineal. Si estableces la ecuación de la línea, podrás predecir cuántas tazas venderás a diferentes precios. ¡Es como tener una bola de cristal para tu negocio!
Ejemplo 2: Trayectoria de un Proyecto
Supón que estás trabajando en un proyecto que tiene un presupuesto limitado y un tiempo específico. Puedes utilizar un plano lineal para representar el progreso del proyecto en función del tiempo. La ecuación podría mostrarte cómo el avance del proyecto (y) se relaciona con el tiempo (x). Si el plano es lineal, significa que el progreso es constante. Pero, ¿y si la línea se curva? Eso podría indicar que estás enfrentando algunos contratiempos. Así que, un simple gráfico puede darte una visión clara de la salud de tu proyecto.
Aplicaciones del Plano Lineal en Diferentes Campos
Economía
Como mencionamos antes, los economistas utilizan planos lineales para modelar la oferta y la demanda. Las curvas de oferta y demanda a menudo se representan como líneas rectas en gráficos, lo que facilita la comprensión de cómo las variaciones en el precio afectan el comportamiento del consumidor y del productor. Es una herramienta poderosa que permite a los economistas hacer predicciones y tomar decisiones informadas.
Física
En física, un plano lineal puede ser utilizado para representar relaciones entre diferentes fuerzas o velocidades. Por ejemplo, en la cinemática, la relación entre la distancia recorrida y el tiempo puede ser lineal si la velocidad es constante. Esto es fundamental para entender el movimiento de los objetos. ¿Te has preguntado alguna vez cómo calcular el tiempo que tardarás en llegar a un lugar? Con un simple plano lineal, puedes hacerlo.
Estadística
La regresión lineal es una técnica estadística que utiliza planos lineales para modelar la relación entre variables. Al analizar conjuntos de datos, los estadísticos pueden determinar si existe una relación significativa entre las variables y, en caso afirmativo, predecir resultados futuros. Esto se aplica en una amplia variedad de campos, desde la medicina hasta el marketing. Así que, si alguna vez has escuchado hablar de «análisis de regresión», ya sabes que se basa en el concepto de planos lineales.
Características del Plano Lineal
Ahora que hemos explorado qué es un plano lineal y sus aplicaciones, hablemos de algunas características clave que lo definen.
Sencillez
Una de las características más atractivas del plano lineal es su simplicidad. La ecuación y = mx + b es fácil de entender y de trabajar. Esto permite a las personas de diferentes disciplinas utilizarlo sin necesidad de ser expertos en matemáticas.
Previsibilidad
Otra característica importante es la previsibilidad que ofrece. Una vez que tienes la ecuación de tu plano, puedes predecir resultados futuros con una buena dosis de confianza. Esto es especialmente útil en entornos de negocios y planificación.
Relación Directa
El plano lineal también refleja relaciones directas entre variables. Esto significa que, si una variable aumenta, la otra también lo hará (o disminuirá) de manera predecible. Esta relación directa es una de las razones por las que es tan utilizado en diferentes campos.
Desafíos y Limitaciones del Plano Lineal
A pesar de todas sus ventajas, el plano lineal no es perfecto. Tiene sus desafíos y limitaciones que es importante considerar.
No Siempre Representa la Realidad
Aunque un plano lineal puede ser útil, no siempre representa con precisión la complejidad del mundo real. Muchas relaciones son no lineales y pueden requerir modelos más sofisticados para ser descritas adecuadamente. Por ejemplo, la relación entre la temperatura y la presión en un gas no es lineal.
Sensibilidad a los Datos Atípicos
Los planos lineales son sensibles a los datos atípicos. Un solo punto de datos fuera de lugar puede distorsionar la línea y llevar a conclusiones erróneas. Por eso es fundamental revisar los datos cuidadosamente antes de aplicar un modelo lineal.
Suposiciones Simplificadas
Los modelos lineales a menudo se basan en suposiciones simplificadas que pueden no ser válidas en todos los casos. Por ejemplo, asumen que la relación entre las variables es constante, lo cual no siempre es cierto en situaciones dinámicas.
En resumen, el plano lineal es una herramienta poderosa y versátil que puede ayudarte a entender las relaciones entre variables en una variedad de contextos. Ya sea que estés analizando datos de ventas, midiendo la velocidad de un objeto o planificando un proyecto, el plano lineal puede ofrecerte una visión clara y sencilla. Sin embargo, es esencial ser consciente de sus limitaciones y estar dispuesto a explorar modelos más complejos cuando sea necesario.
¿El plano lineal es solo para matemáticos?
No, el plano lineal es utilizado en múltiples disciplinas y no es exclusivo para matemáticos. Cualquiera que necesite entender relaciones entre variables puede beneficiarse de él.
¿Cómo puedo graficar un plano lineal?
Para graficar un plano lineal, necesitas determinar la pendiente (m) y la intersección en el eje y (b) de tu ecuación. Luego, traza la línea en un gráfico usando estos puntos.
¿Qué debo hacer si mis datos no se ajustan a una línea recta?
Si tus datos no se ajustan a una línea recta, podrías considerar utilizar modelos no lineales o técnicas de regresión más complejas que se adapten mejor a la naturaleza de tus datos.
¿Dónde puedo encontrar más ejemplos de planos lineales en la vida real?
Los ejemplos de planos lineales son abundantes en la economía, la física y la estadística. Puedes encontrar estudios de caso en libros de texto o en recursos en línea que aborden estos temas.
¿Es el plano lineal la única forma de modelar relaciones entre variables?
No, existen muchos otros métodos para modelar relaciones entre variables, incluidos modelos polinómicos, exponenciales y logarítmicos, entre otros. La elección del modelo depende del contexto y la naturaleza de los datos.
Espero que este artículo te haya proporcionado una comprensión clara y completa sobre el plano lineal. Si tienes más preguntas o deseas profundizar en algún aspecto específico, ¡no dudes en preguntar!