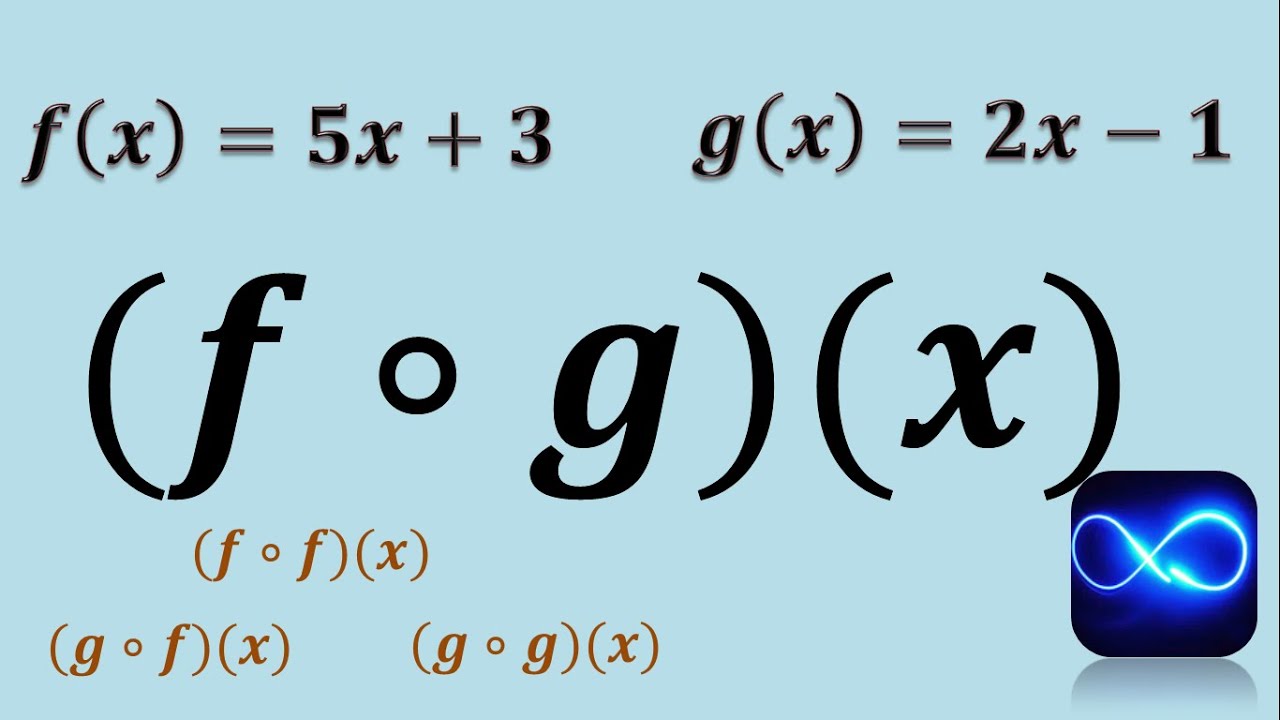La matemática puede parecer un laberinto complicado a veces, ¿no crees? Pero, ¿qué pasaría si te dijera que hay formas de hacer que sea más fácil y divertida? La composición de funciones es uno de esos temas que, aunque puede sonar intimidante al principio, puede volverse un juego interesante una vez que lo entiendes. ¿Te imaginas combinar dos funciones y crear algo nuevo? Es como mezclar dos colores para obtener uno diferente. Vamos a sumergirnos en este fascinante mundo y mejorar nuestras habilidades matemáticas a través de ejercicios prácticos.
¿Qué es la Composición de Funciones?
Antes de entrar en materia, aclaremos qué significa realmente la composición de funciones. Imagina que tienes dos funciones: f(x) y g(x). La composición de estas funciones se denota como f(g(x)). En otras palabras, estás tomando el resultado de g(x) y usándolo como la entrada para f(x). Es un poco como preparar una receta: primero sigues un paso (g) y luego usas el resultado para el siguiente (f). Pero, ¿por qué es importante esto? Porque entender cómo se relacionan las funciones entre sí puede abrirte muchas puertas en matemáticas y en la vida real.
¿Por Qué Practicar Composición de Funciones?
Practicar la composición de funciones es fundamental por varias razones. Primero, te ayuda a comprender mejor cómo funcionan las funciones en general. Te permite ver cómo se interrelacionan y cómo puedes manipularlas para obtener resultados deseados. Además, en áreas como la física, la economía o la ingeniería, las funciones a menudo se combinan para modelar situaciones complejas. Por lo tanto, tener una sólida comprensión de la composición de funciones te equipará mejor para enfrentar problemas en estos campos. Pero, ¿qué tal si empezamos a practicar un poco?
Ejercicios Prácticos de Composición de Funciones
Ejercicio 1: Funciones Simples
Comencemos con algo sencillo. Supongamos que tenemos las funciones f(x) = 2x + 3 y g(x) = x^2. Queremos encontrar f(g(x)). Entonces, primero evaluamos g(x): si x = 2, entonces g(2) = 2^2 = 4. Ahora, tomamos ese resultado y lo introducimos en f(x): f(4) = 2(4) + 3 = 8 + 3 = 11. ¡Listo! Hemos encontrado f(g(2)) = 11.
Ejercicio 2: Combinando Funciones
Ahora, intentemos algo un poco más complicado. Considera las funciones f(x) = 3x – 1 y g(x) = x + 5. Queremos calcular f(g(x)). Primero, evaluamos g(x): si x = 1, entonces g(1) = 1 + 5 = 6. Ahora, sustituyamos ese resultado en f(x): f(6) = 3(6) – 1 = 18 – 1 = 17. Así que f(g(1)) = 17. ¡Qué fácil se vuelve cuando lo desglosas!
Propiedades de la Composición de Funciones
Ahora que hemos practicado un poco, es hora de hablar sobre algunas propiedades interesantes de la composición de funciones. Estas propiedades no solo son útiles para resolver ejercicios, sino que también te ayudarán a entender mejor cómo funcionan las funciones en general.
Propiedad Asociativa
La propiedad asociativa establece que, si tienes tres funciones f, g y h, la composición de funciones no depende del orden en que las combines. Es decir, f(g(h(x))) = (f(g))(h(x)). Esto es como decir que puedes organizar tus tareas de distintas maneras, pero al final, el resultado será el mismo. ¡Qué alivio saber que no tienes que estresarte por el orden!
Identidad de Funciones
La función identidad es otra propiedad fascinante. Si tienes una función f(x) y la combinas con la función identidad i(x) = x, el resultado será f(i(x)) = f(x). Es como decir que si te miras al espejo, no cambias; sigues siendo tú. Esta propiedad puede parecer obvia, pero es crucial para entender cómo funcionan las funciones en el contexto de la composición.
Aplicaciones de la Composición de Funciones
Ahora que hemos cubierto los fundamentos y algunas propiedades, hablemos de cómo se aplica la composición de funciones en el mundo real. Las funciones no son solo números en una hoja de papel; son herramientas que nos ayudan a modelar y entender el mundo que nos rodea.
Modelado en Ciencias
En la física, por ejemplo, la composición de funciones se utiliza para modelar el movimiento. Imagina que estás lanzando una pelota. La altura de la pelota en función del tiempo puede ser una función, mientras que el tiempo en función de la distancia recorrida puede ser otra. Al combinar estas funciones, puedes predecir exactamente dónde aterrizará la pelota. ¡Eso es como tener un superpoder matemático!
Economía y Finanzas
En el mundo de la economía, la composición de funciones también juega un papel crucial. Por ejemplo, si tienes una función que representa el costo de producción y otra que representa la demanda, puedes combinarlas para determinar el precio óptimo de venta. Esto es esencial para maximizar las ganancias y minimizar pérdidas. Así que, la próxima vez que escuches sobre economía, recuerda que las funciones están detrás de cada decisión estratégica.
Consejos para Mejorar en Composición de Funciones
Si quieres volverte un experto en composición de funciones, aquí hay algunos consejos prácticos que puedes seguir. Recuerda, como cualquier habilidad, la práctica es clave.
Practica Regularmente
La práctica regular es fundamental. Resuelve ejercicios de diferentes niveles de dificultad y no te limites a los ejemplos de tu libro de texto. Busca problemas en línea, participa en foros o únete a grupos de estudio. Cuanto más expuesto estés a diferentes tipos de problemas, mejor serás.
Haz Preguntas
No dudes en preguntar cuando algo no esté claro. Hablar con tus compañeros o profesores sobre tus dudas puede abrirte nuevas perspectivas. A veces, una simple explicación puede hacer que todo tenga sentido. ¡No te quedes con la duda!
Utiliza Recursos en Línea
Hoy en día, hay una gran cantidad de recursos en línea disponibles. Desde videos tutoriales hasta ejercicios interactivos, el internet está lleno de herramientas que pueden hacer que aprender sea más entretenido. ¡Aprovecha estas oportunidades y encuentra el método que mejor funcione para ti!
¿Qué es la composición de funciones?
La composición de funciones es el proceso de tomar el resultado de una función y usarlo como entrada para otra. Se representa como f(g(x)).
¿Es la composición de funciones conmutativa?
No, la composición de funciones no es conmutativa. Es decir, f(g(x)) no siempre es igual a g(f(x)).
¿Dónde se aplica la composición de funciones en la vida real?
Se aplica en diversas áreas, como la física para modelar el movimiento, en economía para determinar precios óptimos y en muchas otras disciplinas que utilizan funciones para representar relaciones.
¿Cómo puedo mejorar en composición de funciones?
Practica regularmente, haz preguntas cuando tengas dudas y utiliza recursos en línea para aprender de manera más efectiva.
¿Es difícil aprender sobre la composición de funciones?
Al principio puede parecer complicado, pero con práctica y paciencia, se vuelve más fácil. ¡Recuerda que todos hemos estado allí!
Así que ahí lo tienes, una guía completa sobre la composición de funciones y cómo mejorar en esta área. Recuerda, la clave es la práctica y la curiosidad. ¡Sigue explorando el fascinante mundo de las matemáticas!