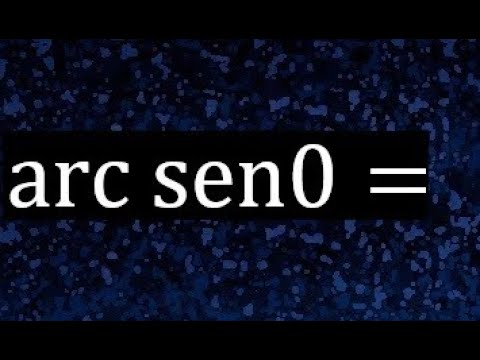¡Hola! Hoy vamos a sumergirnos en el fascinante mundo de las matemáticas, específicamente en el concepto del arcsen. ¿Alguna vez te has preguntado qué significa este término y cómo se aplica en diferentes contextos? Si es así, estás en el lugar correcto. El arcsen, o arco seno, es la función inversa del seno y tiene un papel crucial en la trigonometría y el análisis matemático. Pero, ¿qué pasa cuando hablamos de arcsen de 0? En este artículo, exploraremos su definición, cómo se calcula y algunas aplicaciones prácticas. Prepárate para un viaje lleno de curiosidades matemáticas que, sin duda, te harán ver los números de una manera diferente.
¿Qué es el Arcsen?
Primero, aclaremos qué es el arcsen. La función arcsen es la inversa de la función seno. En otras palabras, si tienes un ángulo y aplicas la función seno, el arcsen te permite recuperar ese ángulo original. Se define como:
y = arcsen(x) significa que x = sen(y), donde y está en el rango de -π/2 a π/2. Así que, si estás pensando en un triángulo rectángulo, el arcsen te ayuda a encontrar el ángulo cuando conoces la razón entre el cateto opuesto y la hipotenusa.
El Arcsen de 0: Definición y Cálculo
Ahora que tenemos una idea de lo que es el arcsen, centrémonos en el arcsen de 0. ¿Qué significa realmente? Cuando decimos arcsen(0), estamos buscando el ángulo cuyo seno es 0. ¿Y cuál es ese ángulo? ¡Exactamente! Es 0 radianes. Así que podemos decir que:
arcsen(0) = 0.
Es importante destacar que el arcsen de 0 es un caso muy especial porque es uno de los pocos valores en la función arcsen que nos da un resultado tan sencillo. Imagina que estás en un plano cartesiano: el punto (0, 0) es donde todo comienza, y el arcsen de 0 representa el ángulo donde la altura (seno) es igual a cero.
¿Por Qué es Relevante el Arcsen de 0?
Entender el arcsen de 0 no es solo un ejercicio académico. Tiene aplicaciones prácticas en diversas áreas, como la física, la ingeniería y la informática. Por ejemplo, al resolver problemas de triángulos o en el análisis de ondas, conocer el arcsen de 0 puede facilitar el proceso de resolución. Además, el arcsen de 0 es fundamental para el cálculo de límites y derivadas en cálculo avanzado.
Aplicaciones Prácticas del Arcsen de 0
Vamos a explorar algunas de las aplicaciones más interesantes del arcsen de 0 en la vida real. ¿Sabías que en la ingeniería eléctrica, el análisis de circuitos a menudo requiere la utilización de funciones trigonométricas? En este contexto, el arcsen puede ayudar a determinar las fases de corriente y voltaje. Por ejemplo, si estás trabajando con un circuito de corriente alterna, el arcsen de 0 te indicará que no hay desfase entre la corriente y el voltaje, lo que es un resultado deseable.
Ejemplo en Física
Imagina que estás lanzando un proyectil. La trayectoria de ese proyectil se puede describir mediante funciones trigonométricas. En este caso, el arcsen de 0 podría usarse para calcular la posición inicial del proyectil en el eje vertical cuando no hay altura. Es como si lanzaras una pelota desde el suelo y quisieras saber el ángulo de lanzamiento que resulta en una altura cero. ¡Fascinante, ¿verdad?!
El Arcsen en el Análisis de Datos
En el mundo de la informática y el análisis de datos, el arcsen se utiliza en algoritmos de machine learning, especialmente en redes neuronales. Aquí, el arcsen de 0 puede aparecer cuando se normalizan datos, ayudando a convertir valores en un rango que sea manejable para el algoritmo. Así que, si alguna vez te has preguntado cómo las máquinas «aprenden», el arcsen juega un papel crucial en ese proceso.
Limitaciones y Consideraciones del Arcsen de 0
Aunque el arcsen de 0 es bastante simple, hay algunas limitaciones que debemos considerar. Por ejemplo, el rango de la función arcsen está restringido entre -π/2 y π/2. Esto significa que si intentamos calcular el arcsen de valores fuera de este rango, no obtendremos resultados válidos. Además, es esencial recordar que la función arcsen no está definida para valores que no están en el rango [-1, 1]. Esto significa que si intentas calcular el arcsen de un número mayor que 1 o menor que -1, te encontrarás con un error.
¿El Arcsen de 0 siempre será 0?
Sí, el arcsen(0) siempre será 0, ya que es el único ángulo cuyo seno es 0 dentro del rango de la función.
¿Se puede calcular el Arcsen de números negativos?
¡Claro! El arcsen también puede calcularse para números negativos, y el resultado estará en el rango de -π/2 a 0.
¿Dónde se utiliza el Arcsen en la vida diaria?
El arcsen se utiliza en muchas áreas, como la ingeniería, la física y la programación, especialmente en problemas que involucran triángulos y ondas.
¿Por qué es importante entender el Arcsen?
Entender el arcsen es fundamental para resolver problemas matemáticos complejos, así como para aplicaciones prácticas en la ciencia y la tecnología.
¿El Arcsen tiene alguna relación con otras funciones trigonométricas?
Definitivamente. El arcsen es la función inversa del seno, y tiene relaciones importantes con el coseno y la tangente, así como con sus respectivas funciones inversas.
En resumen, el arcsen de 0 es un concepto simple pero poderoso en el mundo de las matemáticas. No solo nos ayuda a entender mejor la relación entre los ángulos y los valores del seno, sino que también tiene aplicaciones prácticas en diversas disciplinas. Desde la ingeniería hasta la informática, el arcsen juega un papel crucial en la resolución de problemas y el análisis de datos. Así que, la próxima vez que te encuentres con este término, ¡recuerda que hay un mundo de aplicaciones esperando ser descubierto!