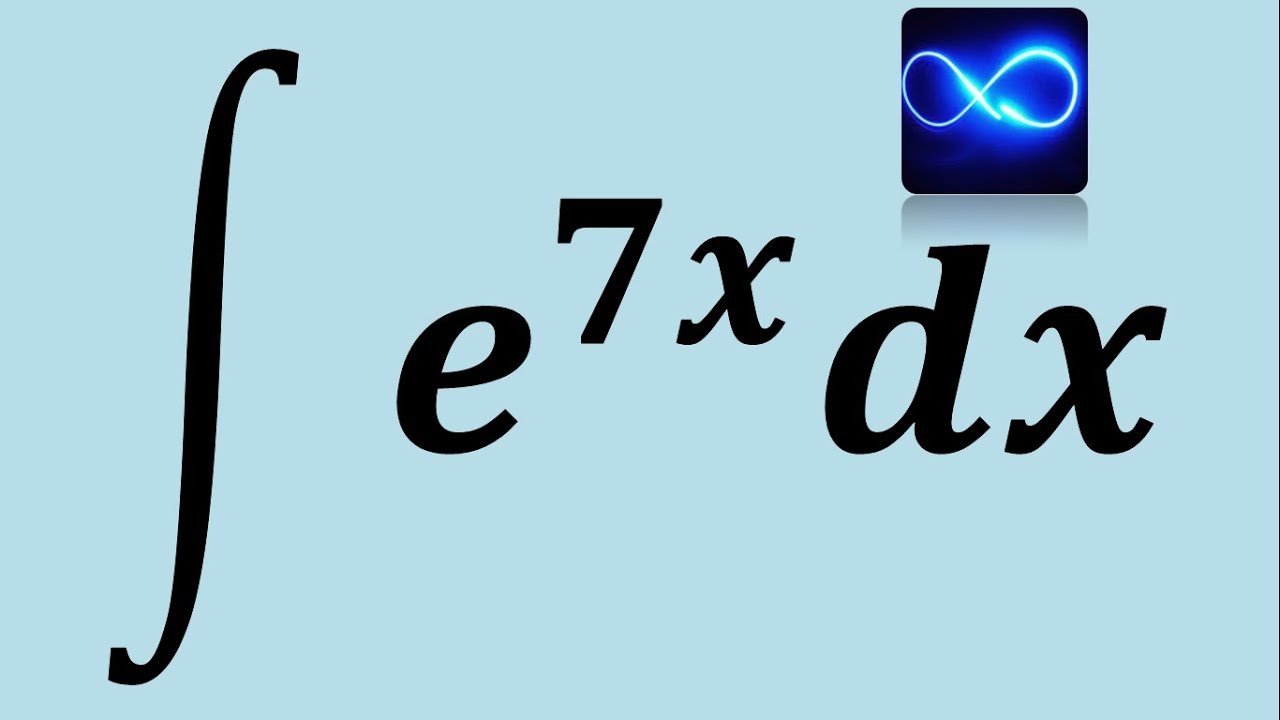¿Alguna vez te has encontrado con un problema matemático que parece un laberinto? Ese momento en que te enfrentas a funciones complicadas y no sabes por dónde empezar. Bueno, hoy vamos a desmitificar uno de esos conceptos que a menudo se sienten como un rompecabezas: la fórmula de integral exponencial. No te preocupes, no es tan aterrador como parece. Vamos a desglosarlo paso a paso y convertir esa confusión en claridad.
¿Qué es la Integral Exponencial?
La integral exponencial, denotada como Ei(x), es una función especial que surge en el cálculo de integrales definidas e indefinidas. Pero, ¿qué significa esto realmente? Imagina que estás tratando de encontrar el área bajo una curva, y esa curva es un poco rebelde, es decir, no se puede integrar de manera sencilla. Aquí es donde la integral exponencial entra en juego como un salvavidas. En términos más técnicos, se define como:
Ei(x) = -∫(-x, ∞) (e^(-t)/t) dt
En otras palabras, la integral exponencial es una forma de expresar la integral de la función exponencial que no se puede resolver con técnicas estándar. Su aplicación es amplia, desde la física hasta la ingeniería y más allá.
¿Por qué es Importante la Integral Exponencial?
La integral exponencial no es solo un concepto abstracto que los matemáticos disfrutan discutir en sus círculos. Tiene aplicaciones prácticas en varios campos. Por ejemplo, en la teoría de circuitos eléctricos, cuando se analiza la respuesta temporal de un circuito, se puede necesitar la integral exponencial. También aparece en la física, especialmente en problemas relacionados con la mecánica cuántica y la estadística. Pero, ¿qué tal si exploramos un poco más sobre cómo se usa?
Aplicaciones en la Física
En el ámbito de la física, la integral exponencial se utiliza para describir fenómenos como la difusión de partículas y el decaimiento radioactivo. Imagina que tienes una sustancia radiactiva que se descompone con el tiempo. La tasa de descomposición no es lineal; en su lugar, sigue un patrón que puede modelarse utilizando la integral exponencial. Esto nos permite predecir cuánto tiempo tomará para que una muestra se reduzca a la mitad, un concepto conocido como la vida media.
Usos en la Ingeniería
Los ingenieros también encuentran la integral exponencial muy útil. Por ejemplo, en el diseño de sistemas de control, las respuestas transitorias de un sistema pueden ser descritas mediante funciones que incluyen la integral exponencial. Esto ayuda a los ingenieros a diseñar sistemas que respondan de manera eficiente a diferentes condiciones de entrada. ¿No es fascinante cómo una función matemática puede tener tanto impacto en el mundo real?
Propiedades de la Integral Exponencial
Ahora que hemos visto algunas aplicaciones, es hora de profundizar en las propiedades de la integral exponencial. Estas propiedades son fundamentales para comprender cómo se comporta esta función y cómo podemos manipularla para resolver problemas.
Conexión con Otras Funciones
Una de las propiedades más interesantes de la integral exponencial es su conexión con otras funciones matemáticas. Por ejemplo, la función logarítmica natural ln(x) está relacionada con Ei(x). Esto es crucial porque nos permite transformar y simplificar problemas complejos en formas más manejables. Además, al analizar el comportamiento de Ei(x) para valores grandes y pequeños de x, podemos obtener información valiosa sobre su naturaleza y sus límites.
Comportamiento Asintótico
El comportamiento asintótico de la integral exponencial es otro aspecto fascinante. A medida que x tiende a infinito, Ei(x) se comporta de manera predecible, lo que nos permite hacer aproximaciones y simplificaciones. Por ejemplo, cuando x es grande, podemos aproximar la integral exponencial de la siguiente manera:
Ei(x) ≈ (e^x/x) + ln(x)
Esto significa que, en ciertos contextos, podemos ignorar términos menos significativos y centrarnos en lo que realmente importa. Es como limpiar un armario: a veces, solo necesitas quedarte con las cosas esenciales y deshacerte del desorden.
Cómo Calcular la Integral Exponencial
Ahora que entendemos qué es la integral exponencial y por qué es importante, hablemos sobre cómo calcularla. Aunque no siempre podemos encontrar una solución analítica sencilla, hay varios métodos que podemos utilizar.
Integración Numérica
Uno de los métodos más comunes es la integración numérica. Esto implica utilizar algoritmos para aproximar el valor de la integral exponencial. Existen diversas técnicas, como el método del trapecio y el método de Simpson, que nos permiten estimar el área bajo la curva de manera efectiva. Aunque no obtendremos un valor exacto, estos métodos son increíblemente útiles en la práctica, especialmente cuando se trabaja con funciones complicadas.
Uso de Software Matemático
En la era digital, también tenemos a nuestra disposición potentes herramientas de software matemático, como MATLAB, Mathematica y Python, que pueden calcular la integral exponencial de manera rápida y precisa. Estas herramientas son como tener una calculadora avanzada en la palma de tu mano, permitiéndote resolver problemas complejos sin tener que recurrir a largas y tediosas derivaciones manuales.
Ejemplos Prácticos
Veamos algunos ejemplos prácticos para ilustrar cómo se aplica la integral exponencial en situaciones reales. Imagina que estás trabajando en un proyecto de ingeniería que involucra la disipación de energía en un circuito. La ecuación que describe la energía disipada puede incluir la integral exponencial, lo que te lleva a utilizar la fórmula para predecir el comportamiento del circuito.
Ejemplo 1: Decaimiento Radiactivo
Supongamos que tienes una muestra de material radiactivo que se descompone a una tasa de 5% por hora. Puedes usar la integral exponencial para modelar la cantidad de material que queda después de un cierto tiempo. Este tipo de cálculo es esencial en campos como la medicina nuclear y la gestión de residuos.
Ejemplo 2: Análisis de Circuitos
En un circuito eléctrico, la respuesta de un capacitor a un voltaje aplicado puede describirse utilizando la integral exponencial. Al analizar cómo cambia la corriente a lo largo del tiempo, los ingenieros pueden diseñar circuitos más eficientes y seguros. Este tipo de análisis es fundamental en la creación de dispositivos electrónicos modernos.
La integral exponencial es un concepto poderoso y versátil que aparece en muchos campos de la ciencia y la ingeniería. Desde su definición hasta sus aplicaciones prácticas, hemos recorrido un camino fascinante a través de este tema. Ahora que tienes una mejor comprensión de la integral exponencial, ¿qué tal si te animas a explorar más sobre este y otros conceptos matemáticos?
1. ¿La integral exponencial tiene aplicaciones fuera de la matemática pura?
¡Definitivamente! La integral exponencial se utiliza en física, ingeniería, estadística y muchas otras disciplinas. Es una herramienta versátil que ayuda a modelar fenómenos en el mundo real.
2. ¿Es posible calcular la integral exponencial manualmente?
Si bien puedes hacerlo en algunos casos simples, la mayoría de las veces es más práctico utilizar métodos numéricos o software especializado para obtener resultados precisos.
3. ¿Existen otras funciones especiales relacionadas con la integral exponencial?
Sí, hay muchas funciones especiales en matemáticas, como la función gamma y la función beta, que también tienen aplicaciones en diversas áreas y están interrelacionadas con la integral exponencial.
4. ¿Cómo puedo mejorar mi comprensión de la integral exponencial?
Una buena manera de mejorar es practicar con problemas y ejemplos, así como utilizar recursos en línea y libros de texto que expliquen el tema en profundidad.
5. ¿La integral exponencial se utiliza en la inteligencia artificial?
Sí, en algunos algoritmos de aprendizaje automático y modelos estadísticos, la integral exponencial puede aparecer en la formulación de ciertos problemas, especialmente en el manejo de distribuciones de probabilidad.