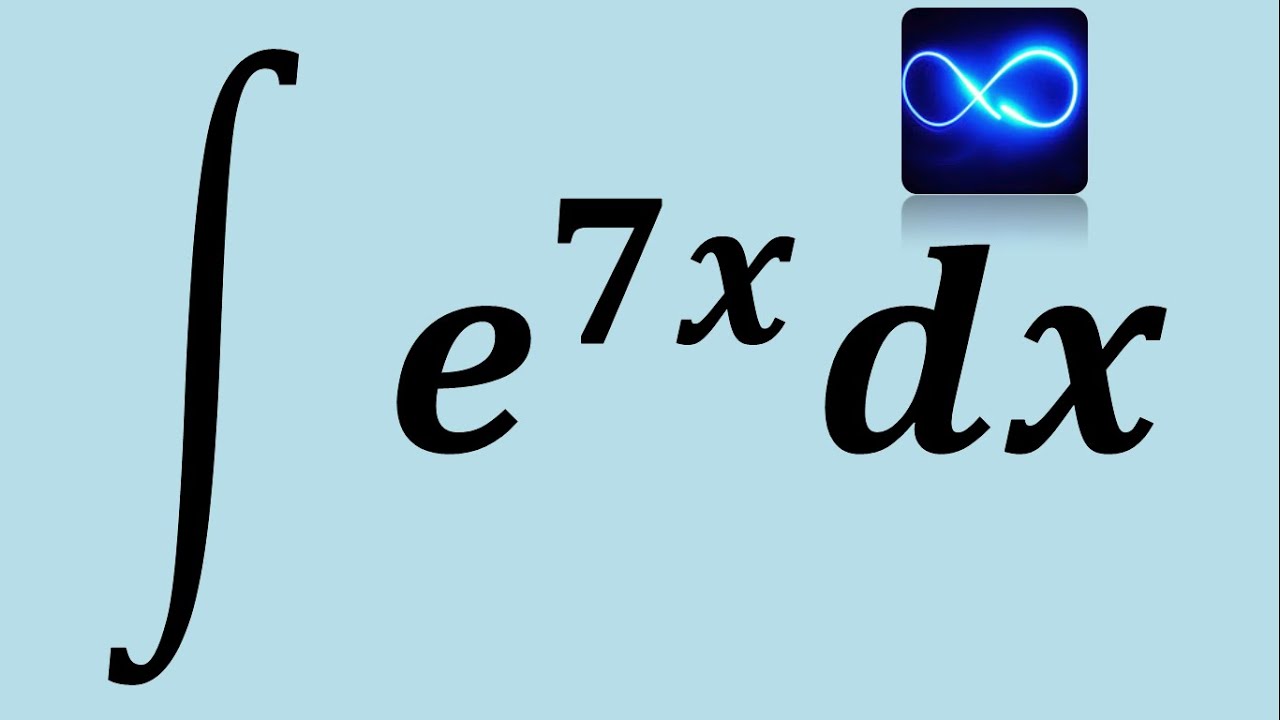Todo lo que Necesitas Saber sobre la Fórmula de Integral Exponencial: Guía Completa y Ejemplos

¡Hola! Si alguna vez te has preguntado cómo se relacionan las integrales con las funciones exponenciales, estás en el lugar correcto. La integral exponencial es un concepto fascinante que aparece en muchas áreas de las matemáticas y la física. Pero no te preocupes, no vamos a sumergirnos en un océano de fórmulas complicadas sin antes entender de qué se trata. En este artículo, desglosaremos la integral exponencial de una manera sencilla y accesible, y te daremos ejemplos prácticos que harán que este concepto cobre vida.

¿Qué es la Integral Exponencial?

La integral exponencial, denotada como Ei(x), es una función especial que se define como la integral del exponencial negativo. En términos más simples, es una forma de expresar el área bajo la curva de la función e^(-t) desde un punto específico hasta el infinito. Pero, ¿por qué deberías preocuparte por esto? Bueno, porque aparece en muchos contextos, desde la física hasta la teoría de probabilidades. Imagina que estás lanzando un proyectil al aire; la integral exponencial puede ayudarte a calcular la trayectoria y el tiempo que tarda en caer. Interesante, ¿verdad?

La Fórmula de la Integral Exponencial

La fórmula básica de la integral exponencial se expresa así:

Ei(x) = -∫(-x) e^(-t) dt

Esta integral no tiene una solución en términos de funciones elementales, pero podemos evaluarla numéricamente o utilizar tablas de valores para obtener resultados específicos. Pero no te preocupes si esto suena un poco intimidante; en los siguientes párrafos, te mostraré cómo puedes trabajar con esta integral de manera práctica.

Propiedades de la Integral Exponencial

Como cualquier función matemática, la integral exponencial tiene propiedades interesantes que vale la pena conocer. Algunas de ellas incluyen:

• Continuidad: La función Ei(x) es continua para todos los valores de x.
• Comportamiento Asintótico: A medida que x se vuelve muy grande, Ei(x) tiende a e^x/x.
• Simetría: Para valores negativos de x, Ei(x) tiene un comportamiento que se puede relacionar con su comportamiento en el lado positivo.

Estas propiedades son útiles cuando intentamos resolver problemas más complejos que involucran la integral exponencial.

Ejemplos Prácticos

Ejemplo 1: Evaluación Numérica

Digamos que queremos evaluar Ei(1). Podemos hacerlo utilizando herramientas de cálculo numérico. Si utilizamos un software matemático o una calculadora avanzada, obtendremos un valor aproximado de:

Ei(1) ≈ 1.71828

Este valor es esencial en diversas aplicaciones, desde la estadística hasta la teoría de circuitos eléctricos. Pero, ¿cómo llegamos a este número sin una calculadora? Aquí es donde entran en juego las tablas de valores de la integral exponencial.

Ejemplo 2: Aplicaciones en la Física

La integral exponencial también aparece en situaciones físicas. Por ejemplo, en el estudio de la desintegración radiactiva, la cantidad de material radiactivo que queda después de un tiempo t puede describirse mediante la función:

N(t) = N0 * e^(-λt)

Donde N0 es la cantidad inicial y λ es la constante de desintegración. Si queremos encontrar el tiempo promedio que tarda en desintegrarse, podemos usar la integral exponencial para calcularlo. Esto demuestra cómo las matemáticas y la física están interconectadas, creando un hermoso mosaico de conocimiento.

Relación con otras Funciones Matemáticas

La integral exponencial no está sola en el mundo de las matemáticas; tiene vínculos con otras funciones especiales. Por ejemplo, está relacionada con la función gamma y la función logarítmica. ¿Alguna vez has oído hablar de la función gamma? Es una extensión del factorial y aparece en la teoría de probabilidades. La relación entre estas funciones se puede ver en varias ecuaciones, lo que demuestra la riqueza de las matemáticas.

La Integral Exponencial y el Cálculo Complejo

Si te interesa el cálculo complejo, la integral exponencial también juega un papel importante allí. En particular, se utiliza en la evaluación de integrales complejas y en la teoría de funciones analíticas. La relación entre la integral exponencial y las funciones complejas es un tema fascinante que vale la pena explorar si te sientes aventurero.

¿Cómo Calcular la Integral Exponencial Manualmente?

Calcular la integral exponencial manualmente puede ser un desafío, pero aquí hay un método paso a paso que puedes seguir:

1. Identifica la función: Determina la función que deseas integrar.
2. Realiza un cambio de variable: Esto puede simplificar la integral. Por ejemplo, si tienes e^(-x), puedes hacer un cambio de variable a t = -x.
3. Evalúa la integral: Usa métodos de integración como integración por partes o sustitución.
4. Consulta tablas o software: Si la integral es complicada, considera usar una tabla de integrales o un software matemático para obtener el resultado.

Aunque puede parecer un proceso tedioso, cada paso es una oportunidad para aprender y comprender más sobre el tema.

Errores Comunes y Cómo Evitarlos

Cuando trabajas con la integral exponencial, es fácil caer en algunos errores comunes. Aquí hay algunos que debes evitar:

• Confundir la integral con la derivada: Asegúrate de no mezclar estos dos conceptos; son opuestos.
• Olvidar el signo negativo: Recuerda que la definición de la integral exponencial implica un signo negativo en la integral.
• Ignorar el contexto: A veces, el contexto del problema puede darte pistas sobre cómo proceder. No subestimes esto.

Si te mantienes alerta y practicas, podrás evitar estos tropiezos y avanzar en tu comprensión de la integral exponencial.

La integral exponencial es más que solo una fórmula; es una herramienta poderosa que abre las puertas a una variedad de aplicaciones en matemáticas, física y más. A medida que sigas explorando este tema, descubrirás que cada concepto está interconectado, creando un rico entramado de conocimiento. Así que, ¿qué esperas? ¡Sumérgete en el mundo de las integrales y descubre todo lo que tienen para ofrecer!

¿La integral exponencial se utiliza en la vida real?

Sí, se utiliza en diversas aplicaciones, desde la ingeniería hasta la estadística. Por ejemplo, en el análisis de circuitos eléctricos y en la modelización de fenómenos naturales.

¿Es difícil entender la integral exponencial?

Como cualquier concepto matemático, puede ser complicado al principio, pero con práctica y ejemplos, se vuelve más comprensible. ¡No te desanimes!

¿Dónde puedo encontrar más recursos sobre la integral exponencial?

Hay muchos libros de texto, tutoriales en línea y videos educativos que pueden ayudarte a profundizar en el tema. Plataformas como Khan Academy y Coursera son excelentes lugares para comenzar.

¿Existen aplicaciones de la integral exponencial en la biología?

¡Definitivamente! En biología, se utiliza en modelos de crecimiento poblacional y en estudios sobre la propagación de enfermedades. La matemática es clave en muchos campos, incluida la biología.

¿Qué software es mejor para calcular integrales exponenciales?

Hay varias opciones, pero algunos de los más populares son MATLAB, Mathematica y Python con bibliotecas como SciPy. Cada uno tiene sus ventajas y desventajas, así que elige el que mejor se adapte a tus necesidades.