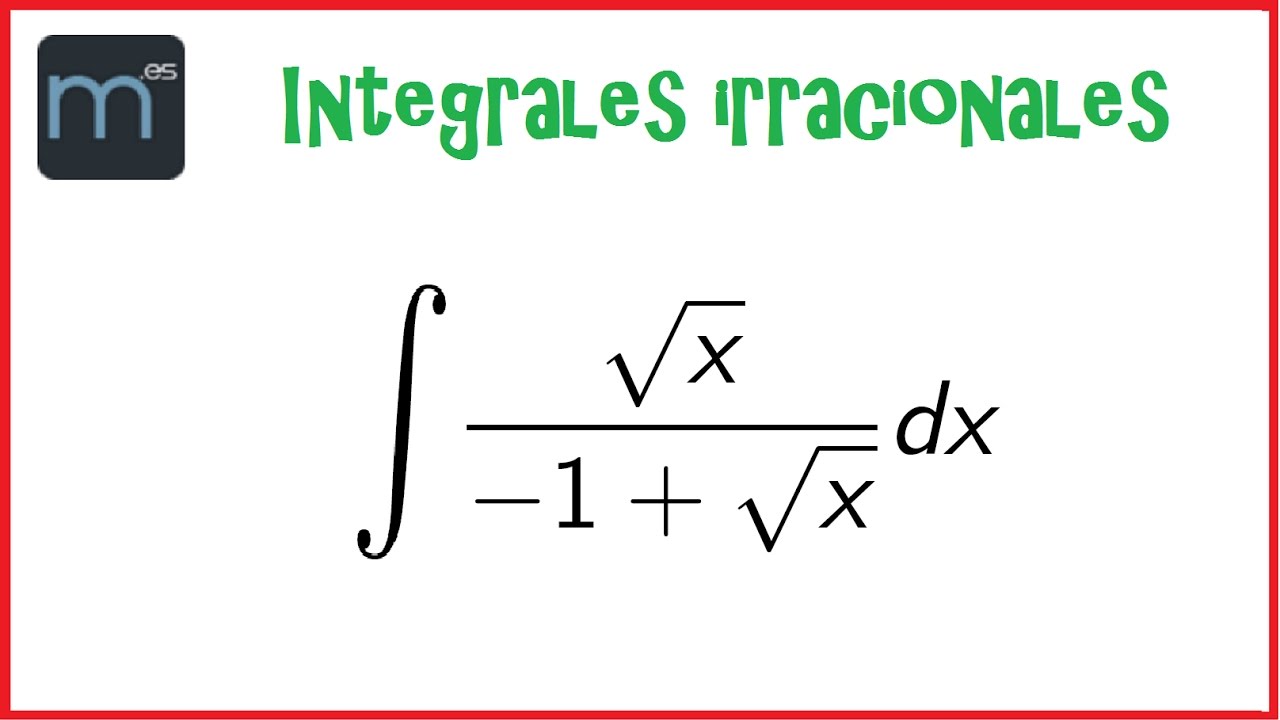¿Alguna vez te has encontrado con una integral que parece un rompecabezas? Las integrales irracionales son esas que nos hacen fruncir el ceño y rascar la cabeza, pero no te preocupes, ¡estás en el lugar correcto! En este artículo, vamos a desglosar todo lo que necesitas saber sobre las integrales irracionales. Desde su definición hasta ejemplos prácticos que te ayudarán a entender mejor este concepto. Así que, si tienes un café en mano y estás listo para sumergirte en el mundo de las matemáticas, ¡vamos a ello!
¿Qué son las Integrales Irracionales?
Las integrales irracionales son aquellas que involucran raíces cuadradas, cúbicas o de cualquier otro tipo que no pueden ser simplificadas a un número racional. ¿Te suena complicado? Imagina que tienes una montaña que escalar, y en lugar de un camino recto, tienes que zigzaguear por senderos empinados. Así es como se siente resolver una integral irracional. En términos matemáticos, una integral irracional puede verse algo así:
∫√(x^2 + 1) dx
En este caso, la expresión bajo la raíz cuadrada no se puede simplificar a un número racional. Las integrales irracionales pueden ser un desafío, pero con las herramientas y técnicas adecuadas, puedes convertirte en un experto en el tema.
Técnicas para Resolver Integrales Irracionales
Ahora que tenemos una idea de qué son las integrales irracionales, hablemos sobre cómo resolverlas. Hay varias técnicas que puedes utilizar, y aquí te presento algunas de las más efectivas:
Sustitución Trigonométrica
La sustitución trigonométrica es como tener un mapa cuando te pierdes en la montaña. Esta técnica es útil cuando tienes expresiones que involucran raíces cuadradas. Por ejemplo, si te enfrentas a la integral:
∫√(1 - x^2) dx
Podrías hacer la sustitución x = sin(θ). Esto transforma la integral en una forma más manejable. Al final, regresarás a la variable original y obtendrás la solución deseada. Es un proceso que requiere práctica, pero ¡no te desanimes!
Integración por Partes
Esta técnica es como desarmar un rompecabezas complicado. A veces, dividir la integral en partes más simples puede facilitar su resolución. La fórmula básica es:
∫u dv = uv - ∫v du
Identifica las partes u y dv en tu integral irracional y aplica la fórmula. A menudo, esto te llevará a una integral más simple que puedes resolver fácilmente.
Ejemplos Prácticos de Integrales Irracionales
Ahora que conoces algunas técnicas, es hora de ponerlas en práctica. Vamos a resolver un par de ejemplos juntos para que veas cómo funcionan.
Ejemplo 1: Integral de una Raíz Cuadrada
Consideremos la integral:
∫√(x^2 + 4) dx
Primero, aplicaremos la sustitución trigonométrica. Tomamos x = 2tan(θ), lo que nos da dx = 2sec²(θ) dθ. Sustituyendo en la integral, obtenemos:
∫√(4tan²(θ) + 4) (2sec²(θ) dθ)
Esto se simplifica a:
4∫sec(θ) dθ
La integral de sec(θ) es ln|sec(θ) + tan(θ)| + C. Finalmente, regresa a la variable original usando la relación entre θ y x. ¡Y voilà! Has resuelto tu primera integral irracional.
Ejemplo 2: Integral de una Raíz Cúbica
Ahora, intentemos con algo un poco más complicado:
∫√(x^3 - 2x) dx
Para resolver esto, podemos usar la integración por partes. Definimos:
u = √(x^3 - 2x) y dv = dx
Calculamos du y v y aplicamos la fórmula de integración por partes. Este proceso puede ser un poco más laborioso, pero con paciencia y práctica, ¡tú puedes hacerlo!
Errores Comunes al Resolver Integrales Irracionales
A medida que te adentras en el mundo de las integrales irracionales, es posible que te encuentres con algunos errores comunes. Aquí hay algunos a los que debes prestar atención:
No Simplificar Correctamente
Es fácil pasar por alto simplificaciones en la expresión. Asegúrate de revisar cada paso y simplificar donde sea posible. A veces, un pequeño error puede llevarte a una solución incorrecta.
Olvidar el C
Recuerda que al integrar, siempre debes añadir la constante de integración C. Es un detalle pequeño, pero crucial. Si lo olvidas, tu respuesta estará incompleta.
¿Por qué son Importantes las Integrales Irracionales?
Puede que te preguntes, “¿por qué debo preocuparme por las integrales irracionales?” La respuesta es simple: ¡son fundamentales en muchas áreas de la ciencia y la ingeniería! Desde la física hasta la economía, las integrales irracionales aparecen en situaciones del mundo real. Así que, aprender a resolverlas te dará herramientas valiosas para tu futuro académico y profesional.
Las integrales irracionales pueden parecer desafiantes, pero con práctica y las técnicas adecuadas, ¡puedes dominarlas! Ya sea utilizando sustituciones trigonométricas o integración por partes, cada paso que tomes te acercará más a convertirte en un experto. Recuerda, la clave es la práctica y la paciencia. Así que, ¡sigue practicando!
¿Qué son las integrales irracionales?
Las integrales irracionales son aquellas que incluyen expresiones que involucran raíces que no se pueden simplificar a números racionales.
¿Cuáles son algunas técnicas para resolver integrales irracionales?
Las técnicas más comunes incluyen la sustitución trigonométrica y la integración por partes.
¿Por qué es importante aprender sobre integrales irracionales?
Son fundamentales en diversas áreas de la ciencia y la ingeniería, y su comprensión puede abrirte puertas en tu carrera académica y profesional.
¿Cómo puedo mejorar en la resolución de integrales irracionales?
La práctica constante es clave. Trabaja en problemas variados y no dudes en revisar tus errores para aprender de ellos.
¿Existen recursos adicionales para aprender sobre integrales irracionales?
Sí, hay muchos libros de texto, videos en línea y plataformas educativas que pueden ayudarte a profundizar en el tema.