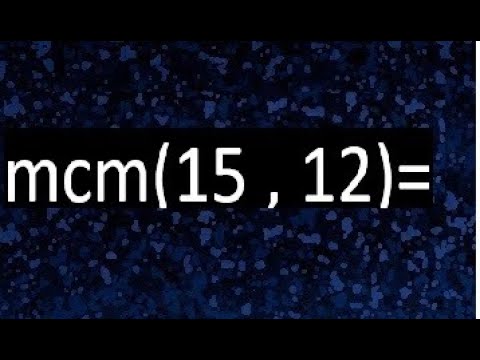¿Alguna vez te has encontrado con números que parecen tener una conexión mágica entre ellos? Eso es exactamente lo que sucede cuando hablamos del Mínimo Común Múltiplo (MCM). En este artículo, vamos a sumergirnos en el fascinante mundo de los números, específicamente en cómo calcular el MCM de 15 y 12. Te prometo que no solo aprenderás a hacerlo, sino que también entenderás por qué es útil y cómo se aplica en la vida diaria. Así que, ¡prepara tu mente matemática y acompáñame en esta aventura numérica!
¿Qué es el MCM?
Antes de lanzarnos a los cálculos, es fundamental que entendamos qué es el MCM. El Mínimo Común Múltiplo es el número más pequeño que es múltiplo de dos o más números. En otras palabras, es como buscar el primer punto de encuentro en un camino que siguen dos amigos. Imagina que uno va a la tienda cada 15 días y el otro cada 12 días; el MCM te dirá cuándo ambos estarán en casa al mismo tiempo.
Pasos para Calcular el MCM de 15 y 12
Ahora que tenemos claro qué es el MCM, vamos a desglosar los pasos para calcularlo. No te preocupes, no es tan complicado como parece. Aquí tienes dos métodos que puedes usar: el método de descomposición en factores primos y el método de listas de múltiplos. Vamos a verlos uno por uno.
Método 1: Descomposición en Factores Primos
Este método puede parecer un poco más técnico, pero es muy efectivo. Vamos a descomponer los números 15 y 12 en sus factores primos.
- 15: Los factores primos de 15 son 3 y 5, ya que 15 = 3 x 5.
- 12: Para 12, los factores primos son 2, 2 y 3, porque 12 = 2 x 2 x 3.
Ahora que tenemos los factores primos, el siguiente paso es tomar todos los factores primos involucrados, usando el mayor exponente que aparece en cualquiera de las descomposiciones.
- De 15, tomamos 31 y 51.
- De 12, tomamos 22 y 31.
Así que, juntando todo esto, el MCM se calcula como:
MCM = 22 x 31 x 51 = 4 x 3 x 5 = 60.
¡Y ahí lo tienes! El MCM de 15 y 12 es 60.
Método 2: Listas de Múltiplos
Si la descomposición en factores primos no es lo tuyo, no hay problema. Puedes usar el método de listas de múltiplos. Este es un enfoque más visual y, a veces, más intuitivo.
Comencemos haciendo listas de múltiplos para ambos números:
- Múltiplos de 15: 15, 30, 45, 60, 75, …
- Múltiplos de 12: 12, 24, 36, 48, 60, 72, …
Ahora, simplemente buscamos el primer número que aparece en ambas listas. ¿Ves ese número brillante? ¡Es 60! Así que, de nuevo, el MCM de 15 y 12 es 60.
¿Por qué es Importante el MCM?
Ahora que sabemos cómo calcular el MCM, puede que te estés preguntando: «¿Para qué sirve todo esto?». Bueno, el MCM es útil en varias situaciones. Por ejemplo, si estás tratando de encontrar un horario común para dos eventos que ocurren en intervalos diferentes, el MCM te dirá cuándo se cruzarán. También se usa en problemas de fracciones para sumar o restar. En resumen, el MCM es una herramienta poderosa en el mundo de las matemáticas y más allá.
Aplicaciones Prácticas del MCM
Imagina que estás organizando una fiesta y quieres asegurarte de que todos los amigos lleguen a la misma hora. Si uno de ellos llega cada 15 minutos y otro cada 12 minutos, el MCM te ayudará a encontrar la mejor hora para que todos estén juntos. O piensa en un escenario escolar: si tienes dos clases que se repiten en diferentes días, el MCM te dirá cuándo habrá una coincidencia.
Ejemplos de la Vida Real
Para que lo veas más claro, aquí tienes un par de ejemplos de la vida real:
- Imagina que tienes un reloj que suena cada 15 minutos y otro que suena cada 12 minutos. ¿Cuándo sonarán juntos? La respuesta, como ya sabemos, es cada 60 minutos.
- Supón que tienes dos máquinas en una fábrica que producen piezas a intervalos de 15 y 12 minutos. El MCM te dirá cada cuánto tiempo ambas máquinas habrán producido el mismo número de piezas.
Consejos para Practicar el Cálculo del MCM
Ahora que tienes una comprensión básica del MCM, aquí hay algunos consejos para practicar y mejorar tus habilidades:
- Intenta calcular el MCM de otros pares de números usando ambos métodos. Esto te ayudará a reforzar tu comprensión.
- Juega con aplicaciones en línea o juegos matemáticos que se centren en el MCM.
- Explica el concepto a alguien más. A veces, enseñar es la mejor forma de aprender.
1. ¿El MCM siempre es mayor que los números originales?
No necesariamente. Si uno de los números es un múltiplo del otro, el MCM será el número más grande. Por ejemplo, el MCM de 6 y 12 es 12.
2. ¿Puedo usar el MCM en más de dos números?
¡Claro! Puedes calcular el MCM de tres o más números. Simplemente aplica el mismo proceso y usa el MCM de dos números a la vez hasta que todos estén incluidos.
3. ¿Cuál es la diferencia entre el MCM y el MCD?
El MCM es el mínimo común múltiplo, mientras que el MCD es el máximo común divisor. Ambos son útiles en diferentes contextos matemáticos.
4. ¿Hay una fórmula rápida para calcular el MCM?
Sí, hay una relación entre el MCM y el MCD que dice que MCM(a, b) = (a * b) / MCD(a, b). Esto puede ser útil si ya conoces el MCD.
5. ¿Por qué el MCM es importante en matemáticas?
El MCM es fundamental para resolver problemas de fracciones, optimizar horarios y comprender patrones en números. Es una herramienta esencial en la teoría de números.
Así que, ya lo sabes, calcular el MCM de 15 y 12 no solo es posible, sino también muy práctico. ¡Ahora es tu turno de ponerlo en práctica!