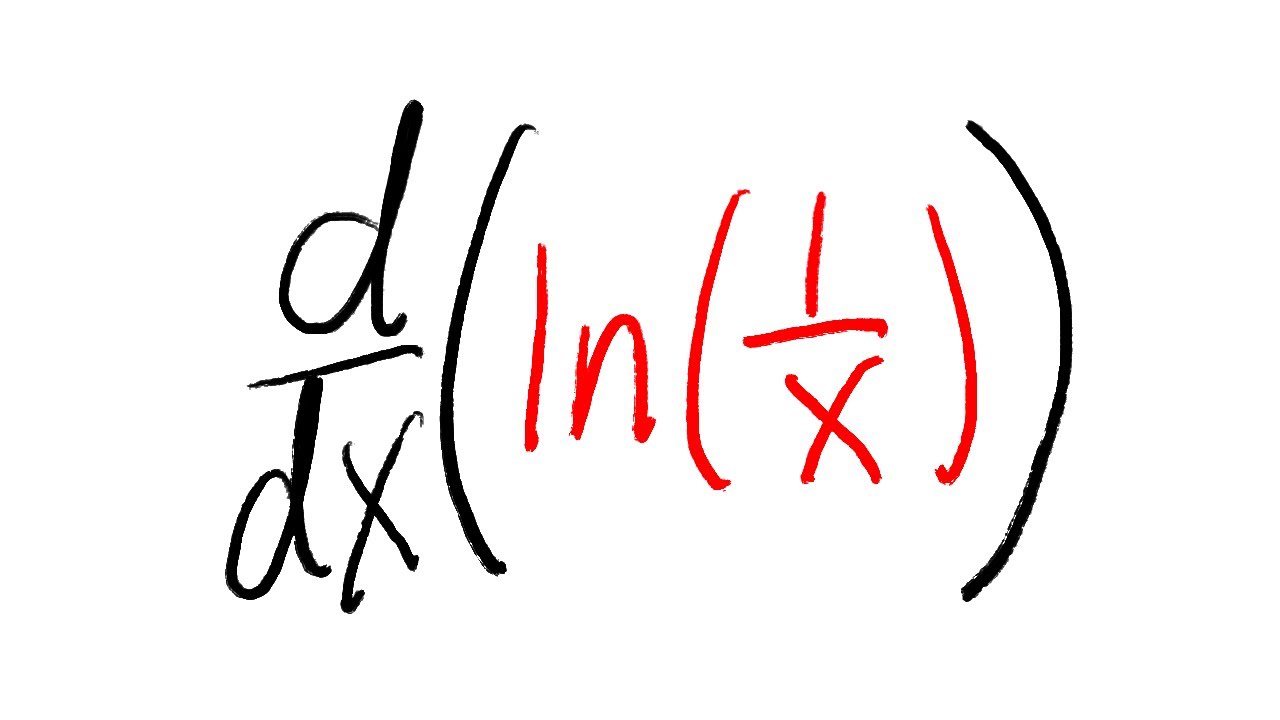¿Alguna vez te has encontrado con la función ln(1/x) y te has preguntado cómo calcular su derivada? Si es así, ¡estás en el lugar correcto! La derivada es una herramienta fundamental en el cálculo, que nos permite entender cómo cambian las funciones. En este artículo, vamos a desglosar el proceso para que puedas calcular la derivada de ln(1/x) de manera sencilla y comprensible. No te preocupes, no necesitas ser un genio de las matemáticas para seguir este paso a paso. Así que, ¡vamos a ello!
¿Qué es ln(1/x)?
Antes de sumergirnos en la derivada, es importante entender qué significa ln(1/x). La función ln(x) es el logaritmo natural de x, y se basa en la base del número e (aproximadamente 2.71828). Cuando decimos ln(1/x), estamos hablando del logaritmo natural del recíproco de x. Pero, ¿qué significa esto en términos más simples? Imagina que tienes una pizza. Si decides compartirla entre tus amigos, el recíproco de la cantidad de pizza que cada uno recibe es como tomar el logaritmo de esa cantidad. En este caso, ln(1/x) te da una forma de medir cuánta pizza le queda a cada amigo en función de cuántos son.
Reglas Básicas de Derivación
Antes de calcular la derivada de ln(1/x), repasemos algunas reglas básicas de derivación que nos serán útiles. La regla más relevante aquí es la regla de la cadena, que nos dice cómo derivar una función compuesta. Además, la derivada de ln(u) es 1/u * (du/dx), donde u es una función de x. Esta regla nos permitirá descomponer la función ln(1/x) para calcular su derivada de manera efectiva.
Aplicando la Regla de la Cadena
Ahora que tenemos las reglas en mente, vamos a aplicar la regla de la cadena a nuestra función ln(1/x). Primero, podemos reescribir ln(1/x) usando propiedades de logaritmos. Sabemos que ln(1/x) es lo mismo que ln(x^(-1)). Usando las propiedades de logaritmos, esto se convierte en -ln(x). ¡Más sencillo, verdad? Ahora, podemos calcular la derivada de -ln(x) en lugar de ln(1/x).
Calculando la Derivada de -ln(x)
La derivada de ln(x) es 1/x. Por lo tanto, al derivar -ln(x), simplemente multiplicamos por -1. Así que, la derivada de -ln(x) es -1/x. ¡Y ahí lo tenemos! La derivada de ln(1/x) es -1/x. Pero, ¿por qué detenernos aquí? Vamos a profundizar un poco más en el significado de esta derivada.
Interpretando la Derivada
¿Qué significa realmente que la derivada de ln(1/x) sea -1/x? En términos prácticos, esto nos dice que a medida que x aumenta, el valor de ln(1/x) disminuye. Esto tiene sentido si piensas en cómo funciona el logaritmo natural. A medida que x se hace más grande, 1/x se hace más pequeño, lo que significa que el logaritmo de un número más pequeño también será más negativo. La derivada, entonces, nos da una tasa de cambio: por cada aumento en x, la función ln(1/x) disminuye a un ritmo de -1/x.
Ejemplos Prácticos
Veamos un par de ejemplos prácticos para solidificar nuestra comprensión. Supongamos que tenemos x = 2. Si calculamos ln(1/2), obtenemos aproximadamente -0.693. Ahora, si aumentamos x a 3, ln(1/3) es aproximadamente -1.099. La diferencia en los valores es significativa, y al calcular la derivada, podemos ver que -1/x nos da una tasa de cambio que refleja esta disminución.
Más Allá de ln(1/x)
Ahora que hemos cubierto la derivada de ln(1/x), es interesante considerar cómo este concepto se aplica a otras funciones logarítmicas. Las funciones logarítmicas son bastante comunes en matemáticas y ciencia, y entender cómo calcular sus derivadas puede ser muy útil. Por ejemplo, ¿qué pasaría si tuviéramos que calcular la derivada de ln(x^2)? Aquí, aplicaríamos la misma regla de la cadena, y obtendríamos 2/x como resultado.
Comparación con Otras Funciones
Comparar ln(1/x) con otras funciones logarítmicas nos ayuda a ver patrones en el cálculo de derivadas. Por ejemplo, la derivada de ln(x) es 1/x, y la derivada de ln(x^2) es 2/x. La función ln(1/x) es un caso especial que nos enseña cómo la manipulación de funciones puede llevar a resultados interesantes.
En resumen, calcular la derivada de ln(1/x) no es tan complicado como parece. Con un poco de comprensión sobre las propiedades de los logaritmos y las reglas de derivación, puedes abordar este tipo de problemas con confianza. La clave es descomponer la función en partes más manejables y aplicar las reglas adecuadas.
Recuerda que la derivada nos da una visión de cómo cambian las funciones, y entender este concepto puede abrir muchas puertas en el mundo del cálculo y más allá. Ahora que has aprendido cómo calcular la derivada de ln(1/x), ¿te sientes más preparado para enfrentar otros desafíos matemáticos?
¿Qué significa la derivada en términos prácticos?
La derivada nos dice cómo cambia una función en relación con su variable independiente. En el caso de ln(1/x), nos indica cómo disminuye la función a medida que x aumenta.
¿Puedo aplicar el mismo método para otras funciones logarítmicas?
¡Sí! Las mismas reglas de derivación se aplican a otras funciones logarítmicas. Solo necesitas ajustar la función que estás derivando.
¿Por qué es importante entender las derivadas?
Las derivadas son fundamentales en matemáticas y ciencia, ya que nos ayudan a analizar el comportamiento de funciones, optimizar problemas y modelar fenómenos del mundo real.
¿Qué otras funciones debo conocer para derivar correctamente?
Es útil familiarizarse con las funciones polinómicas, exponenciales y trigonométricas, así como con las reglas de derivación, como la regla del producto y la regla del cociente.
¿Hay alguna aplicación práctica de la derivada de ln(1/x)?
Sí, en economía, la derivada de funciones logarítmicas puede ayudar a entender el crecimiento y decrecimiento de variables, como la oferta y la demanda. También se utiliza en ingeniería y ciencias naturales para modelar cambios en sistemas.
¡Y ahí lo tienes! Un recorrido completo por el proceso de derivar ln(1/x). Espero que ahora te sientas más cómodo con este concepto. ¿Listo para el próximo desafío matemático?