Las funciones exponenciales son uno de esos conceptos matemáticos que pueden parecer intimidantes al principio, pero una vez que los entiendes, se convierten en una herramienta poderosa. ¿Alguna vez te has preguntado cómo crecen las poblaciones o cómo se comporta el dinero en una cuenta de ahorros? Todo esto se puede explicar mediante funciones exponenciales. Así que, si estás listo para sumergirte en el fascinante mundo de las matemáticas, acompáñame en este recorrido. Vamos a desglosar estos conceptos y ejercicios para que no solo los entiendas, sino que también los domines.
¿Qué es una Función Exponencial?
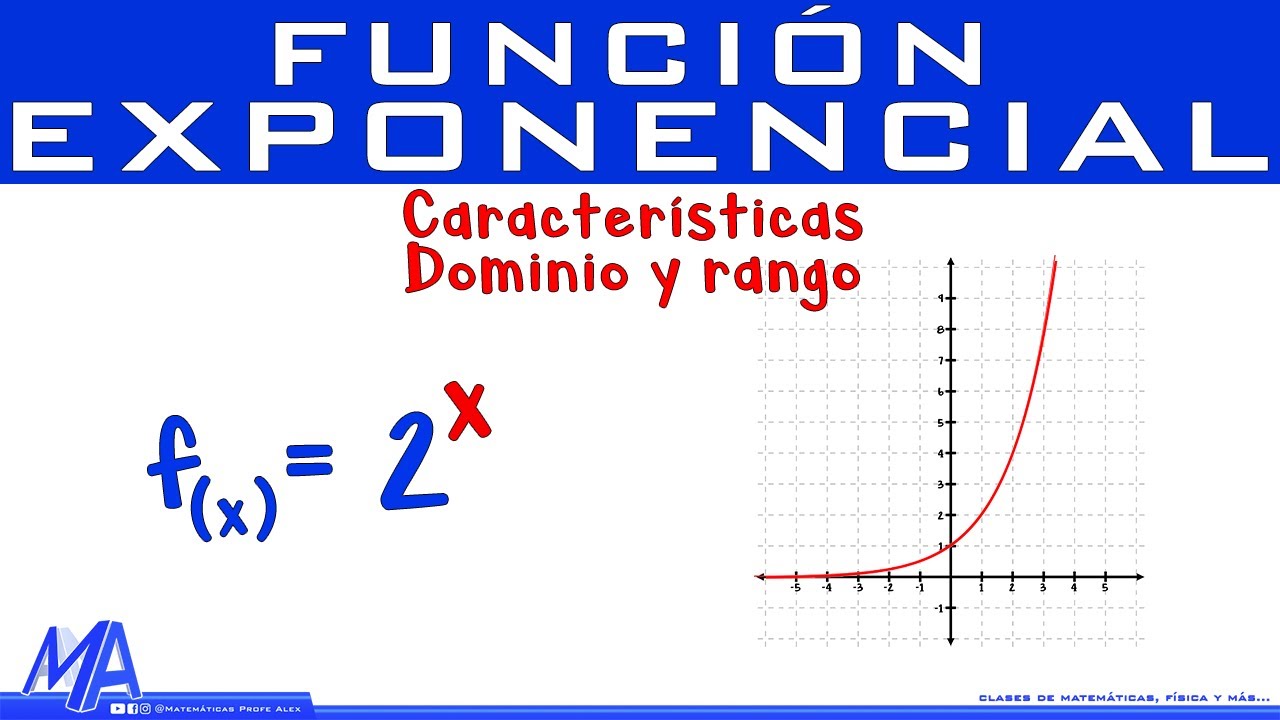
Una función exponencial es una función de la forma f(x) = a * b^x, donde a es una constante, b es la base de la exponencial (un número positivo distinto de 1), y x es la variable. Esta función tiene algunas características fascinantes. Por ejemplo, si b > 1, la función crecerá rápidamente; si 0 < b < 1, la función disminuirá rápidamente. Esto puede ser visualizado como una montaña que se eleva hacia el cielo o como una colina que se hunde hacia el suelo.
Características Clave de las Funciones Exponenciales
Para que puedas tener una idea clara, aquí hay algunas características clave:
- Crecimiento Rápido: A medida que x aumenta, f(x) se eleva a alturas inesperadas.
- Intercepto en el Eje Y: Siempre cruza el eje y en el punto (0, a).
- Dominio y Rango: El dominio es todos los números reales, pero el rango es solo números positivos.
Ejercicios Prácticos para Dominar Funciones Exponenciales
Ahora que hemos cubierto lo básico, es hora de poner manos a la obra. La práctica es fundamental, así que aquí tienes algunos ejercicios que te ayudarán a comprender mejor las funciones exponenciales.
Ejercicio 1: Graficando una Función Exponencial
Comencemos con algo visual. Toma la función f(x) = 2^x. ¿Puedes graficarla? Comienza por calcular algunos puntos:
- Cuando x = -2, f(-2) = 2^{-2} = 0.25
- Cuando x = -1, f(-1) = 2^{-1} = 0.5
- Cuando x = 0, f(0) = 2^{0} = 1
- Cuando x = 1, f(1) = 2^{1} = 2
- Cuando x = 2, f(2) = 2^{2} = 4
Ahora, une esos puntos y observa cómo se comporta la función. ¿Ves cómo se eleva rápidamente a medida que te mueves hacia la derecha? Eso es el crecimiento exponencial en acción.
Ejercicio 2: Resolviendo Ecuaciones Exponenciales
Pasemos a algo un poco más desafiante. Resolvamos la ecuación 3^x = 81. ¿Cómo lo harías? Aquí tienes un truco: puedes reescribir 81 como una potencia de 3. Sabemos que 81 = 3^4, así que la ecuación se convierte en 3^x = 3^4. Ahora, ¿qué puedes deducir de esto? Exacto, ¡x debe ser igual a 4!
Aplicaciones de las Funciones Exponenciales
Las funciones exponenciales no son solo un concepto abstracto; tienen aplicaciones en el mundo real que son fascinantes. Desde la biología hasta la economía, aquí hay algunas áreas donde verás estas funciones en acción.
Crecimiento Poblacional
Imagina una colonia de bacterias que se duplica cada hora. Si comienzas con 100 bacterias, después de una hora tendrás 200, después de dos horas tendrás 400, y así sucesivamente. Este tipo de crecimiento se puede modelar con una función exponencial. ¡Es como si estuvieras viendo una película de acción donde las bacterias son los protagonistas!
Intereses Compuestos
Si alguna vez has ahorrado dinero en un banco, has experimentado el poder de las funciones exponenciales. El interés compuesto se calcula utilizando una fórmula exponencial, lo que significa que tu dinero crece más rápido a medida que pasa el tiempo. Es como plantar una semilla y ver cómo se convierte en un árbol gigante, gracias a la magia del interés compuesto.
Desafíos Adicionales
Si sientes que ya has dominado lo básico, aquí tienes algunos desafíos adicionales para poner a prueba tus habilidades:
Desafío 1: Encuentra el Crecimiento Exponencial
Supón que una inversión de $500 crece a una tasa del 5% anual. ¿Cuánto tendrás después de 10 años? Utiliza la fórmula del interés compuesto A = P(1 + r)^t, donde P es el capital inicial, r es la tasa de interés y t es el tiempo en años.
Desafío 2: Aplicaciones en la Vida Real
Investiga sobre el uso de funciones exponenciales en la tecnología, como en la computación cuántica o en la predicción de epidemias. ¿Cómo se utilizan estas funciones para modelar situaciones complejas?
Las funciones exponenciales son un tema apasionante que se presenta en muchos aspectos de nuestra vida diaria. Desde el crecimiento de poblaciones hasta las finanzas, su comprensión puede ofrecerte una nueva perspectiva sobre cómo funciona el mundo. Así que no te detengas aquí; sigue practicando y explorando. ¿Qué tal si te desafías a ti mismo a encontrar más ejemplos de funciones exponenciales en tu entorno? Recuerda, la práctica hace al maestro.
¿Por qué son importantes las funciones exponenciales?
Las funciones exponenciales son fundamentales en diversas disciplinas, como la biología, la economía y la física, ya que ayudan a modelar fenómenos que involucran crecimiento o decrecimiento acelerado.
¿Cómo puedo practicar más sobre funciones exponenciales?
Existen numerosos recursos en línea, como plataformas de aprendizaje, videos y ejercicios interactivos. También puedes crear tus propios problemas basados en situaciones del mundo real.
¿Qué diferencia hay entre crecimiento exponencial y lineal?
El crecimiento lineal aumenta a un ritmo constante, mientras que el crecimiento exponencial aumenta a un ritmo que se acelera con el tiempo, lo que resulta en un crecimiento mucho más rápido.
¿Se pueden aplicar funciones exponenciales a otros campos?
Definitivamente. Las funciones exponenciales se utilizan en campos como la química para modelar reacciones, en la física para estudiar la desintegración radiactiva, y en la informática para entender algoritmos complejos.
¿Cómo se pueden representar gráficamente las funciones exponenciales?
Las funciones exponenciales se representan gráficamente mostrando cómo el valor de f(x) cambia a medida que varía x. Generalmente, la gráfica muestra un crecimiento rápido hacia la derecha y se aproxima al eje x a medida que se mueve hacia la izquierda.
Este artículo busca ser informativo y accesible, utilizando un tono conversacional y proporcionando ejemplos y ejercicios para ayudar a comprender mejor el tema de las funciones exponenciales.