¿Alguna vez te has preguntado cómo crecen ciertas poblaciones o cómo se descomponen los materiales? Las funciones exponenciales son fundamentales para entender estos fenómenos. En este artículo, vamos a desglosar todo lo que necesitas saber sobre las funciones exponenciales, desde su definición hasta ejercicios resueltos que te ayudarán a dominar el tema. ¡Prepárate para sumergirte en un mundo donde las matemáticas cobran vida!
¿Qué son las Funciones Exponenciales?
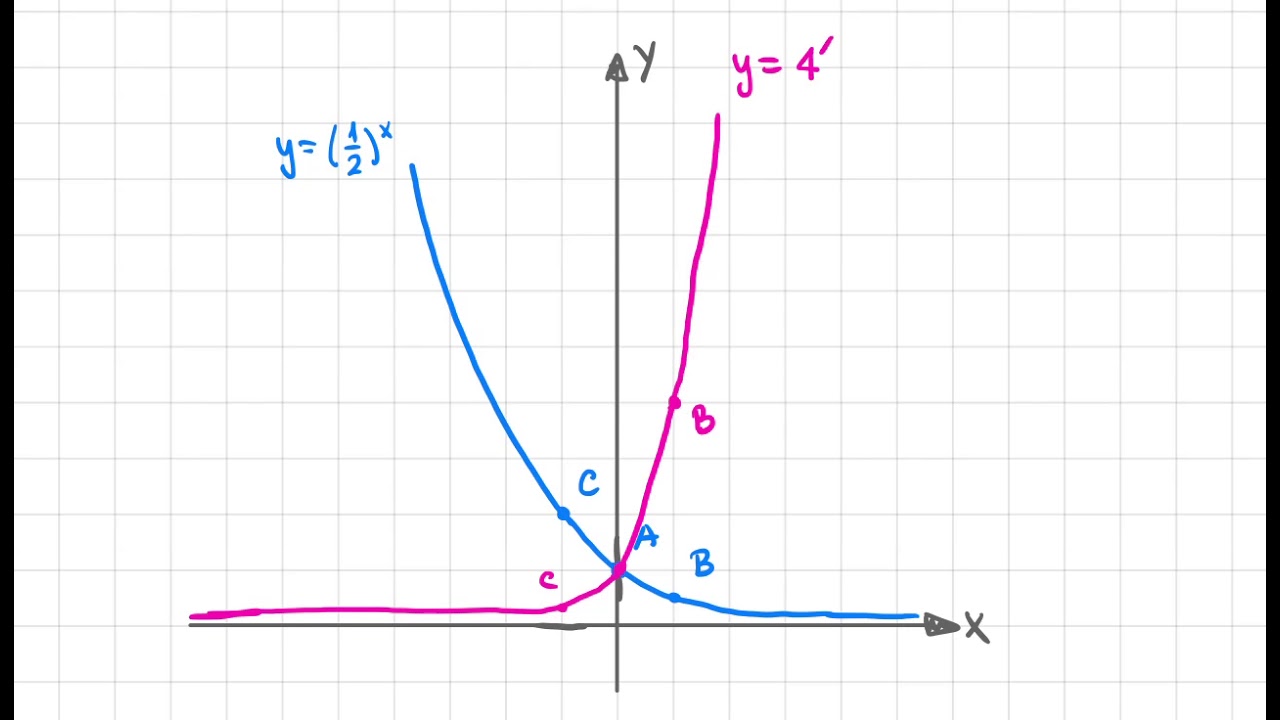
Las funciones exponenciales son aquellas en las que una variable independiente aparece en el exponente. La forma general de una función exponencial es f(x) = a * b^x, donde a es un coeficiente constante, b es la base de la exponencial (un número positivo diferente de 1), y x es la variable. Imagina que a representa la cantidad inicial de algo, como una población, y b es la tasa de crecimiento. Si piensas en un árbol que crece a un ritmo constante, su altura puede ser representada por una función exponencial. Fascinante, ¿verdad?
Características de las Funciones Exponenciales
Las funciones exponenciales tienen varias características interesantes que las hacen únicas:
- Crecimiento Rápido: A medida que
xaumenta, el valor def(x)crece rápidamente. Piensa en el crecimiento de una población de conejos, que puede duplicarse en poco tiempo. - Dominio y Rango: El dominio de las funciones exponenciales es todos los números reales, mientras que el rango es siempre positivo. No puedes tener una cantidad negativa de conejos, ¿verdad?
- Intersección con el Eje Y: La función siempre intersecta el eje Y en el punto (0, a). Esto significa que cuando
x=0,f(0)=a.
Ejemplo Gráfico de Funciones Exponenciales
Imagina que graficas f(x) = 2^x. Al principio, cuando x es negativo, los valores de f(x) son pequeños, pero a medida que x se vuelve positivo, los valores empiezan a dispararse. Este comportamiento es lo que hace que las funciones exponenciales sean tan interesantes y útiles en diversas áreas, desde la biología hasta la economía.
Ejercicios Resueltos de Funciones Exponenciales
Ahora que ya tenemos una buena base, es hora de practicar. A continuación, resolveremos algunos ejercicios juntos. Recuerda, la práctica es clave para dominar cualquier tema.
Ejercicio 1: Cálculo de una Función Exponencial
Supongamos que tienes la función f(x) = 3 * 2^x. ¿Cuál es el valor de f(4)? Para resolverlo, simplemente sustituimos x por 4:
f(4) = 3 * 2^4 = 3 * 16 = 48
Así que, f(4) = 48. ¡Sencillo, ¿verdad?
Ejercicio 2: Crecimiento Poblacional
Imagina que una población de bacterias se duplica cada hora y comienza con 50 bacterias. La función que representa este crecimiento es f(t) = 50 * 2^t, donde t es el tiempo en horas. ¿Cuántas bacterias habrá después de 5 horas?
f(5) = 50 * 2^5 = 50 * 32 = 1600
Por lo tanto, después de 5 horas, tendrás 1600 bacterias. ¡Eso es un montón de bacterias!
Ejercicio 3: Descomposición Radiactiva
Por otro lado, las funciones exponenciales también se utilizan para modelar la descomposición de materiales radiactivos. Supongamos que tienes un material que se descompone a la mitad cada 3 años. Si comienzas con 80 gramos, la función sería f(t) = 80 * (1/2)^(t/3). ¿Cuánto quedará después de 9 años?
f(9) = 80 * (1/2)^(9/3) = 80 * (1/2)^3 = 80 * (1/8) = 10
Después de 9 años, te quedarán 10 gramos del material. ¡La ciencia es impresionante!
Aplicaciones de las Funciones Exponenciales
Las funciones exponenciales no son solo una curiosidad matemática; tienen aplicaciones prácticas en el mundo real. Vamos a ver algunas de ellas.
Crecimiento de Poblaciones
Las funciones exponenciales son utilizadas para modelar el crecimiento de poblaciones. Por ejemplo, si una población de animales crece de manera exponencial, puedes predecir cuántos habrá en el futuro utilizando una función exponencial. Este tipo de modelado es crucial para la conservación de especies y la gestión de recursos naturales.
Intereses Compuestos en Finanzas
En el ámbito financiero, las funciones exponenciales se utilizan para calcular el interés compuesto. Cuando depositas dinero en una cuenta de ahorros, el interés se calcula sobre el monto total, lo que significa que tu dinero crece de manera exponencial. ¡Imagina que tu dinero trabaja para ti mientras duermes!
Biología y Farmacología
En biología, las funciones exponenciales pueden describir la proliferación celular o la eliminación de fármacos del cuerpo. Comprender cómo se comportan estas funciones puede ser vital para desarrollar tratamientos y medicamentos eficaces.
Errores Comunes al Trabajar con Funciones Exponenciales
Al aprender sobre funciones exponenciales, es común cometer algunos errores. Aquí hay algunos que debes evitar:
- Confundir la base: Asegúrate de no mezclar las bases. Recuerda que
bdebe ser mayor que 0 y diferente de 1. - Olvidar el coeficiente inicial: No olvides el valor de
aal evaluar la función. A menudo se pasa por alto, pero es esencial para obtener el resultado correcto. - Desestimar el contexto: Al resolver problemas del mundo real, siempre considera el contexto. Una función puede tener diferentes significados dependiendo de la situación.
Las funciones exponenciales son una parte fascinante de las matemáticas que se manifiestan en muchas áreas de la ciencia y la vida cotidiana. Desde el crecimiento de poblaciones hasta las finanzas, su comprensión es fundamental para interpretar el mundo que nos rodea. Así que, la próxima vez que veas una función exponencial, ¡recuerda lo que has aprendido aquí!
¿Qué es una función exponencial en términos simples?
Una función exponencial es una función matemática donde la variable se encuentra en el exponente, lo que genera un crecimiento o decrecimiento rápido dependiendo de la base utilizada.
¿Cómo puedo saber si una función es exponencial?
Si la variable está en el exponente y la base es un número positivo distinto de 1, entonces es una función exponencial. Por ejemplo, f(x) = 3 * 2^x.
¿Las funciones exponenciales siempre crecen?
No necesariamente. Si la base es menor que 1, la función decrece. Por ejemplo, en f(x) = 5 * (1/2)^x, a medida que x aumenta, f(x) disminuye.
¿Dónde se aplican las funciones exponenciales en la vida real?
Se utilizan en diversas áreas, incluyendo biología (crecimiento de poblaciones), finanzas (interés compuesto) y física (descomposición radiactiva).
¿Por qué es importante estudiar funciones exponenciales?
Entender funciones exponenciales te ayuda a interpretar fenómenos naturales y procesos matemáticos, lo que es esencial en muchas disciplinas científicas y prácticas.