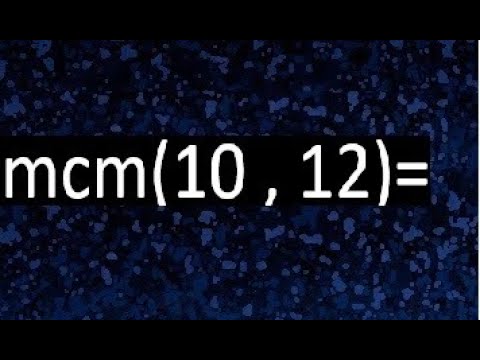Entendiendo el Mínimo Común Múltiplo (MCM)
¿Alguna vez te has preguntado cómo se relacionan los números en el mundo de las matemáticas? Bueno, ¡estás en el lugar correcto! Hoy vamos a hablar sobre el Mínimo Común Múltiplo (MCM), específicamente de los números 10 y 12. El MCM es una herramienta fundamental en matemáticas que nos ayuda a resolver problemas de fracciones, sumas y muchas otras áreas. Pero no te preocupes, no vamos a sumergirnos en un océano de fórmulas complicadas. En su lugar, exploraremos este concepto de manera sencilla y amena. Así que, siéntate, relájate y acompáñame en este viaje numérico.
Para comenzar, definamos qué es el MCM. En términos simples, el MCM de dos o más números es el múltiplo más pequeño que todos esos números comparten. Por ejemplo, si tomamos los números 10 y 12, queremos encontrar el primer número que se pueda dividir por ambos sin dejar un residuo. Imagina que estás organizando una fiesta y necesitas saber cuántas sillas comprar para que todos se sienten cómodamente. El MCM te ayudará a asegurarte de que no falten sillas ni sobre. Ahora, veamos cómo podemos calcular el MCM de 10 y 12 de manera fácil y divertida.
¿Cómo se Calcula el Mínimo Común Múltiplo?
Existen varios métodos para calcular el MCM, y aquí te presentaré dos de los más comunes. Primero, hablemos del método de descomposición en factores primos. Este método puede parecer un poco técnico, pero lo desglosaremos en pasos simples.
Método de Descomposición en Factores Primos
1. Descomponer los números en factores primos: Para encontrar el MCM, primero descomponemos cada número en sus factores primos. Para el número 10, sus factores primos son 2 y 5 (10 = 2 × 5). Para el número 12, sus factores primos son 2, 2 y 3 (12 = 2 × 2 × 3 o 2² × 3).
2. Tomar el máximo exponente de cada factor: Ahora, tomamos cada factor primo y buscamos el mayor exponente que aparece en la descomposición de ambos números. En nuestro caso, tenemos:
– Para el 2: el mayor exponente es 2 (de 12).
– Para el 3: el mayor exponente es 1 (de 12).
– Para el 5: el mayor exponente es 1 (de 10).
3. Multiplicar los factores: Ahora multiplicamos estos factores con sus máximos exponentes:
– MCM = 2² × 3¹ × 5¹ = 4 × 3 × 5 = 60.
Así que, ¡ahí lo tienes! El MCM de 10 y 12 es 60. Es como encontrar el punto de encuentro perfecto entre dos amigos que tienen horarios diferentes, y ambos pueden coincidir en un momento ideal.
Método de Listado de Múltiplos
Si no te gusta mucho la descomposición, no te preocupes. También puedes encontrar el MCM listando los múltiplos de cada número. Este método es más visual y, a veces, más intuitivo.
1. Listar los múltiplos: Empezamos por listar algunos múltiplos de 10 y 12:
– Múltiplos de 10: 10, 20, 30, 40, 50, 60, 70, …
– Múltiplos de 12: 12, 24, 36, 48, 60, 72, …
2. Buscar el mínimo común: Ahora, simplemente buscamos el primer número que aparece en ambas listas. Si observas, el primer número que se repite es 60.
Y, ¡voilà! De nuevo, el MCM de 10 y 12 es 60. Este método es como hacer una búsqueda del tesoro: estás buscando ese tesoro oculto en la lista de números.
Aplicaciones del Mínimo Común Múltiplo
Ahora que sabemos cómo calcular el MCM, hablemos de por qué es importante. El MCM tiene varias aplicaciones en la vida diaria y en diferentes áreas de las matemáticas. Aquí hay algunas maneras en las que puede ser útil.
Sumas y Restas de Fracciones
Uno de los usos más comunes del MCM es en las fracciones. Cuando queremos sumar o restar fracciones que tienen denominadores diferentes, necesitamos un denominador común. El MCM nos proporciona ese denominador. Por ejemplo, si quieres sumar 1/10 y 1/12, necesitas convertir ambas fracciones a un denominador común, que en este caso es 60. Así que, el MCM no solo es un número, ¡es una herramienta que facilita las operaciones matemáticas!
Resolviendo Problemas de Tiempo
Imagina que tienes dos relojes que suenan en diferentes intervalos: uno cada 10 minutos y otro cada 12 minutos. Si quieres saber cada cuánto tiempo sonarán al mismo tiempo, necesitas encontrar el MCM de esos dos números. En este caso, el MCM de 10 y 12 es 60, lo que significa que ambos relojes sonarán juntos cada 60 minutos. ¡Es una forma de organizar tu tiempo!
En la Vida Cotidiana
Además de las aplicaciones matemáticas, el MCM también se encuentra en situaciones cotidianas. Piensa en la planificación de eventos. Si estás organizando un evento que tiene dos actividades que se repiten a intervalos diferentes, el MCM te ayudará a determinar cuándo ambas actividades se llevarán a cabo simultáneamente. Esto puede ser útil para no perderte nada emocionante.
Consejos para Recordar el Mínimo Común Múltiplo
Si bien el MCM puede parecer complicado al principio, hay algunos consejos que pueden ayudarte a recordarlo y aplicarlo de manera efectiva.
Practica con Diferentes Números
La práctica hace al maestro. Cuanto más practiques encontrar el MCM de diferentes números, más fácil se volverá. Intenta hacerlo con números pequeños y luego avanza a números más grandes. ¡Es como aprender a andar en bicicleta! Al principio puede ser difícil, pero con el tiempo te volverás un experto.
Usa Recursos Visuales
Utiliza diagramas o tablas para visualizar los múltiplos. Esto puede hacer que el proceso sea más fácil y divertido. A veces, ver las cosas en un formato visual puede ayudar a que la información se asiente mejor en tu mente.
Hazlo Divertido
Intenta convertir el aprendizaje del MCM en un juego. Puedes desafiar a tus amigos o familiares a encontrar el MCM de diferentes números y ver quién puede hacerlo más rápido. ¡La competencia puede hacer que aprender sea más emocionante!
¿El Mínimo Común Múltiplo siempre es mayor que los números originales?
No necesariamente. El MCM de dos números puede ser igual a uno de ellos si uno es múltiplo del otro. Por ejemplo, el MCM de 4 y 8 es 8.
¿Se puede encontrar el MCM de más de dos números?
¡Por supuesto! Puedes encontrar el MCM de tres o más números usando el mismo proceso. Simplemente descompón cada número en factores primos o lista sus múltiplos y sigue el mismo principio.
¿Qué pasa si los números son primos entre sí?
Si los números son primos entre sí, su MCM será simplemente el producto de ambos números. Por ejemplo, el MCM de 3 y 5 es 15, ya que no tienen factores primos en común.
¿El MCM es lo mismo que el Máximo Común Divisor (MCD)?
No, el MCM y el MCD son conceptos diferentes. El MCD es el número más grande que divide a ambos números, mientras que el MCM es el número más pequeño que es múltiplo de ambos. ¡Es como comparar manzanas con naranjas!
¿Puedo usar calculadoras para encontrar el MCM?
Sí, muchas calculadoras y herramientas en línea pueden ayudarte a encontrar el MCM rápidamente. Sin embargo, es bueno entender el proceso manualmente para que puedas aplicar el conocimiento en diferentes situaciones.
Ahora que hemos explorado el Mínimo Común Múltiplo de 10 y 12, espero que te sientas más cómodo con este concepto. Recuerda que el MCM no solo es un número; es una herramienta útil que puedes aplicar en diversas áreas de la vida cotidiana. Ya sea que estés resolviendo fracciones, organizando eventos o simplemente explorando el fascinante mundo de los números, el MCM siempre estará ahí para ayudarte. ¡Así que sigue practicando y divirtiéndote con las matemáticas!