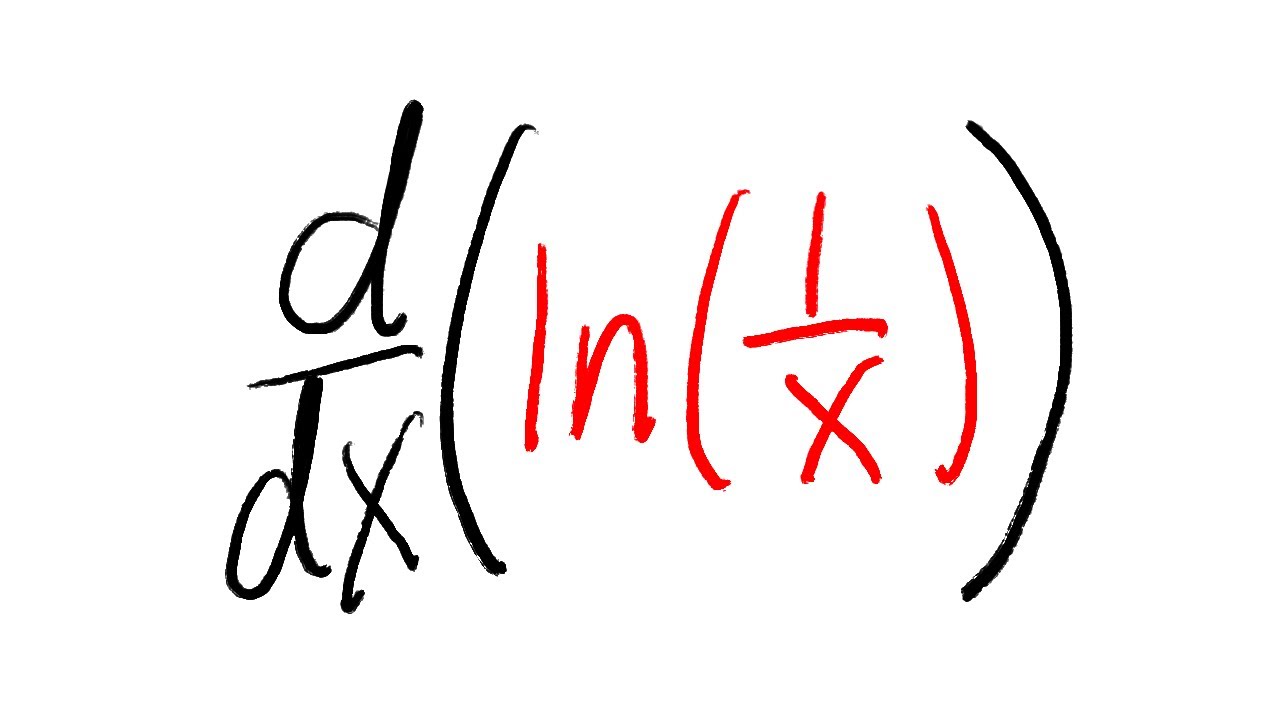Calcular la derivada de una función puede parecer un desafío, pero no te preocupes, ¡estamos aquí para desglosarlo paso a paso! Hoy vamos a explorar cómo derivar la función ln(1/x). Antes de entrar en detalles, hagamos una pequeña pausa para entender qué significa realmente derivar una función. En términos simples, la derivada de una función nos dice cómo cambia esa función en un punto específico. Imagina que estás conduciendo: la derivada es como el velocímetro de tu coche, que te dice cuán rápido estás yendo en un instante determinado. Entonces, ¿estás listo para convertirte en un experto en derivadas? ¡Vamos allá!
Entendiendo la Función ln(1/x)
Primero, necesitamos descomponer la función ln(1/x). La función logarítmica natural, ln, tiene propiedades interesantes que facilitan su manipulación. En este caso, podemos aplicar una de esas propiedades: ln(a/b) = ln(a) – ln(b). Esto significa que podemos reescribir ln(1/x) como ln(1) – ln(x). Ahora, ln(1) es igual a 0, así que nos queda simplemente -ln(x). ¡Así que hemos simplificado la tarea desde el principio!
Reescribiendo la Función
Entonces, nuestra función original ln(1/x) se transforma en -ln(x). Esto es útil porque ahora podemos aplicar las reglas de derivación de manera más sencilla. Recuerda, la derivada de ln(x) es 1/x. Pero, como nuestra función es -ln(x), también debemos considerar el signo negativo. Esto es un detalle crucial, y aquí es donde muchos pueden perderse. ¡No te preocupes! Vamos a profundizar en cómo calcular esta derivada.
Aplicando la Regla de Derivación
Ahora que tenemos nuestra función como -ln(x), es hora de calcular la derivada. Usamos la regla básica de derivación que mencionamos antes. La derivada de -ln(x) es -1/x. Así que, ¡bingo! Hemos encontrado nuestra respuesta. Pero, ¿qué significa esto en términos prácticos? Significa que la tasa de cambio de la función ln(1/x) es -1/x. Es como si estuvieras viendo cómo se desacelera el coche a medida que avanzas. A medida que x aumenta, la derivada se hace más pequeña, lo que indica que la función se está acercando a cero. Fascinante, ¿verdad?
Visualizando la Derivada
Una buena manera de entender la derivada es visualizándola. Imagina que tienes un gráfico de la función -ln(x). La curva comienza alta y se va aplanando a medida que x aumenta. La derivada, -1/x, nos muestra que, aunque la función sigue bajando, lo hace a un ritmo cada vez más lento. Puedes imaginarlo como una montaña que se va desmoronando; al principio, hay mucho material que se desmorona, pero a medida que la montaña se vuelve más pequeña, la cantidad de material que cae también disminuye. Esto es lo que la derivada nos está diciendo sobre el comportamiento de la función.
Aplicaciones Prácticas de la Derivada
Ahora que hemos calculado la derivada, es importante preguntarnos: ¿dónde podemos aplicar este conocimiento? Las derivadas son herramientas fundamentales en muchas áreas, desde la física hasta la economía. Por ejemplo, en la economía, las derivadas pueden ayudarte a entender cómo los cambios en el precio de un producto afectan la demanda. En la física, pueden describir cómo la velocidad de un objeto cambia con el tiempo. Así que, conocer cómo derivar funciones logarítmicas como ln(1/x) no solo es útil en matemáticas, sino que tiene aplicaciones prácticas en el mundo real.
Ejercicios Prácticos
Para realmente afianzar tu comprensión, aquí tienes un par de ejercicios prácticos. Intenta calcular la derivada de las siguientes funciones:
- ln(2/x)
- ln(3/x^2)
Recuerda aplicar la propiedad logarítmica que discutimos y no olvides el signo negativo. Cuando termines, ¡compara tus respuestas con la solución que te daré a continuación!
Soluciones a los Ejercicios
Ahora, vamos a resolver los ejercicios que propusimos antes:
- Para ln(2/x), lo reescribimos como ln(2) – ln(x). La derivada es 0 – 1/x = -1/x.
- Para ln(3/x^2), lo reescribimos como ln(3) – 2ln(x). La derivada es 0 – 2(1/x) = -2/x.
¡Espero que hayas llegado a las mismas respuestas! Si no, no te desanimes. Cada error es una oportunidad para aprender.
¿Por qué se utiliza el logaritmo natural en cálculo?
El logaritmo natural tiene propiedades únicas que facilitan el cálculo de derivadas y se relaciona directamente con el crecimiento exponencial, lo que lo hace ideal en muchas aplicaciones matemáticas.
¿Qué pasa si tengo una función más complicada?
Para funciones más complejas, puedes combinar las reglas de derivación, como la regla del producto o la regla de la cadena. Siempre es útil descomponer la función en partes más manejables.
¿Dónde puedo practicar más problemas de derivadas?
Hay muchos recursos en línea, como Khan Academy o Wolfram Alpha, donde puedes encontrar ejercicios y problemas para practicar. También puedes buscar libros de cálculo que ofrezcan problemas resueltos y ejercicios.
¿Es necesario entender la derivada de ln(1/x) para aprender cálculo?
No es estrictamente necesario, pero entender cómo derivar funciones logarítmicas es muy útil y te dará una buena base para abordar problemas más complejos en cálculo.
Y así, hemos llegado al final de nuestra guía sobre cómo calcular la derivada de ln(1/x). Espero que ahora te sientas más seguro en tus habilidades de derivación y que puedas aplicar este conocimiento en tus estudios. ¡Sigue practicando y nunca dejes de aprender!