¿Alguna vez te has preguntado cómo se relacionan dos variables que parecen estar en constante tira y afloja? Esa es la esencia de la proporcionalidad inversa. En términos simples, cuando una variable aumenta, la otra disminuye, y viceversa. Imagínate que tienes un frasco lleno de agua. Si decides verter más agua en el frasco, el espacio que queda para el aire disminuye. En este caso, el volumen de agua y el volumen de aire están en proporción inversa. Es un concepto que puede parecer un poco abstracto al principio, pero te prometo que es más fácil de entender de lo que parece.
La proporcionalidad inversa se expresa matemáticamente como ( y = frac{k}{x} ), donde ( k ) es una constante. Esto significa que si multiplicas ( x ) por un número, ( y ) se divide por ese mismo número. En otras palabras, si duplicas el valor de ( x ), el valor de ( y ) se reduce a la mitad. Este tipo de relación se puede observar en muchos aspectos de la vida diaria, desde la física hasta la economía. Así que, acompáñame en este viaje donde exploraremos la definición, ejemplos y aplicaciones de la proporcionalidad inversa.
Definición de Proporcionalidad Inversa
Cuando hablamos de proporcionalidad inversa, nos referimos a una relación específica entre dos variables. En este tipo de relación, el producto de las dos variables es constante. Es decir, si una variable aumenta, la otra necesariamente debe disminuir para que el producto total se mantenga igual. Es como una balanza; si un lado se eleva, el otro lado debe bajar para que todo permanezca equilibrado. Esta relación es fundamental en diversas disciplinas, como la física, la economía y la biología.
Para ilustrar esto con un ejemplo sencillo, imagina que estás llenando un tanque de agua. Cuanto más rápido abres el grifo (mayor flujo de agua), menos tiempo tardarás en llenar el tanque. Aquí, el tiempo y el flujo de agua son inversamente proporcionales. Si decides abrir el grifo a la mitad de la velocidad, tardarás el doble de tiempo en llenar el tanque. Este tipo de relación es muy común y se puede ver en diferentes contextos, desde la velocidad y el tiempo de viaje hasta la cantidad de trabajadores y el tiempo requerido para completar una tarea.
Ejemplos Cotidianos de Proporcionalidad Inversa
Ahora que tenemos una idea clara de qué es la proporcionalidad inversa, veamos algunos ejemplos cotidianos que te ayudarán a comprender mejor este concepto.
Ejemplo 1: Velocidad y Tiempo
Imagina que tienes que recorrer una distancia de 100 kilómetros. Si conduces a una velocidad de 100 km/h, tardarás una hora en llegar a tu destino. Pero, si decides conducir a 50 km/h, tardarás 2 horas. En este caso, la velocidad y el tiempo están en relación de proporcionalidad inversa. Si aumentas la velocidad, el tiempo disminuye.
Ejemplo 2: Precio y Cantidad
Supón que estás comprando manzanas. Si el precio por kilo es de 5 euros y decides comprar 2 kilos, pagarás 10 euros. Pero si el precio baja a 2 euros por kilo, puedes comprar 5 kilos por el mismo monto. Aquí, el precio por kilo y la cantidad comprada son inversamente proporcionales. Cuando el precio baja, la cantidad que puedes comprar aumenta.
Ejemplo 3: Luz y Distancia
Otro ejemplo interesante se puede observar en la iluminación. Cuanto más lejos te alejas de una fuente de luz, menos iluminado está el área a tu alrededor. Si te acercas a la luz, el área iluminada aumenta. En este caso, la intensidad de la luz y la distancia están en relación inversa. A medida que te alejas, la intensidad disminuye.
Aplicaciones de la Proporcionalidad Inversa
La proporcionalidad inversa no solo es un concepto teórico; tiene aplicaciones prácticas en varias áreas. Vamos a explorar algunas de ellas.
Aplicaciones en Física
En física, la ley de gravitación universal es un excelente ejemplo de proporcionalidad inversa. La fuerza de gravedad entre dos objetos es inversamente proporcional al cuadrado de la distancia entre ellos. Esto significa que, a medida que te alejas de un objeto masivo, la fuerza gravitacional que sientes disminuye rápidamente. Es como si el universo estuviera jugando al escondite; cuanto más lejos estés, menos sentirás su tirón.
Aplicaciones en Economía
En el mundo de la economía, la ley de la oferta y la demanda también refleja una relación de proporcionalidad inversa. Cuando el precio de un producto aumenta, la demanda tiende a disminuir, y viceversa. Imagina que estás en un mercado y ves que el precio de las fresas se dispara. Probablemente, pensarás dos veces antes de comprarlas, lo que resulta en una disminución de la demanda. Este equilibrio es fundamental para entender cómo funcionan los mercados.
Aplicaciones en Biología
En biología, la proporcionalidad inversa se puede observar en la relación entre el tamaño de un organismo y su tasa de metabolismo. Generalmente, los organismos más pequeños tienen tasas metabólicas más altas que los más grandes. Por ejemplo, un ratón tiene un metabolismo mucho más rápido que un elefante. Esto significa que, a medida que aumenta el tamaño del organismo, la tasa de metabolismo disminuye.
Matemáticas de la Proporcionalidad Inversa
Ahora que hemos cubierto ejemplos y aplicaciones, es momento de profundizar un poco más en la parte matemática de la proporcionalidad inversa. ¿Te parece?
La Ecuación
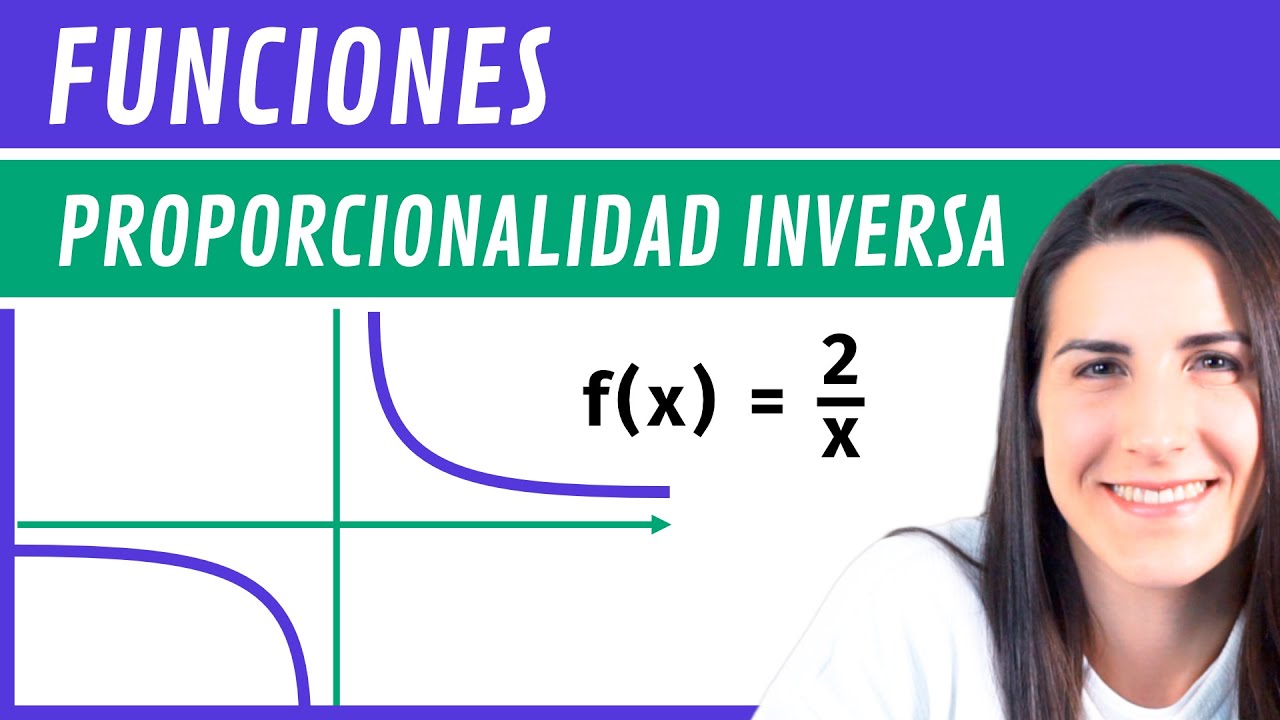
La ecuación básica de la proporcionalidad inversa es ( y = frac{k}{x} ). Aquí, ( k ) es una constante que representa el producto de ( x ) y ( y ). Si deseas graficar esta relación, verás que la gráfica tendrá la forma de una hipérbola, lo que refleja cómo ( y ) disminuye a medida que ( x ) aumenta.
Resolver Problemas de Proporcionalidad Inversa
Supongamos que tienes el siguiente problema: si ( y ) es 10 cuando ( x ) es 5, ¿cuánto vale ( y ) cuando ( x ) es 10? Primero, determina ( k ) usando la relación original:
( k = y cdot x = 10 cdot 5 = 50 )
Ahora, usa este valor de ( k ) para encontrar ( y ) cuando ( x = 10 ):
( y = frac{k}{x} = frac{50}{10} = 5 )
Por lo tanto, cuando ( x ) es 10, ( y ) es 5. ¡Así de sencillo!
¿Por Qué es Importante Comprender la Proporcionalidad Inversa?
Entender la proporcionalidad inversa no solo es útil para resolver problemas matemáticos, sino que también nos ayuda a comprender mejor el mundo que nos rodea. Desde la forma en que interactuamos con nuestro entorno hasta cómo tomamos decisiones económicas, este concepto es fundamental. Al reconocer estas relaciones, podemos tomar decisiones más informadas y anticipar las consecuencias de nuestras acciones.
Imagina que estás en un negocio y decides aumentar los precios de tus productos. Si comprendes la proporcionalidad inversa, sabrás que esto podría llevar a una disminución en la demanda, lo que a su vez podría afectar tus ganancias. Este tipo de pensamiento crítico es invaluable en cualquier ámbito de la vida.
¿La proporcionalidad inversa se aplica solo en matemáticas?
No, la proporcionalidad inversa se encuentra en diversas disciplinas, como la física, la economía y la biología. Es un concepto que nos ayuda a entender cómo interactúan diferentes variables en el mundo real.
¿Cómo puedo identificar una relación de proporcionalidad inversa en un problema?
Para identificar una relación de proporcionalidad inversa, busca situaciones donde el aumento de una variable causa la disminución de otra. También puedes usar la ecuación ( y = frac{k}{x} ) para verificar si las variables cumplen con esta relación.
¿Qué otros ejemplos puedo encontrar de proporcionalidad inversa en la vida diaria?
Además de los ejemplos mencionados, puedes encontrar proporcionalidad inversa en situaciones como la relación entre la cantidad de trabajadores y el tiempo necesario para completar un proyecto, o entre la presión y el volumen de un gas en física.
¿Es la proporcionalidad inversa lo mismo que la proporcionalidad directa?
No, son conceptos opuestos. En la proporcionalidad directa, ambas variables aumentan o disminuyen juntas, mientras que en la proporcionalidad inversa, una variable aumenta mientras la otra disminuye.
¿Cómo se relaciona la proporcionalidad inversa con la hipérbola?
La gráfica de una relación de proporcionalidad inversa tiene la forma de una hipérbola, lo que significa que a medida que una variable aumenta, la otra disminuye de manera no lineal.
Con esto, espero haberte ayudado a entender mejor la proporcionalidad inversa. Si tienes más preguntas, no dudes en preguntar. ¡Siempre hay más por descubrir!