¿Alguna vez te has preguntado cómo saber si dos rectas se cruzan, son paralelas o coinciden? La posición relativa de dos rectas es un tema fascinante en geometría que no solo es esencial para las matemáticas, sino que también tiene aplicaciones en la vida real, como en la arquitectura y el diseño gráfico. En este artículo, te guiaré a través de este concepto, desglosando todo lo que necesitas saber y proporcionando ejemplos prácticos que te ayudarán a entenderlo de manera sencilla y efectiva. Así que, ¡prepárate para sumergirte en el mundo de las rectas!
## ¿Qué Son las Rectas?
Antes de entrar en materia, vamos a asegurarnos de que estamos en la misma página. Una recta, en términos matemáticos, es una línea recta que se extiende infinitamente en ambas direcciones. En el plano cartesiano, cada recta puede ser representada mediante una ecuación lineal de la forma (y = mx + b), donde (m) es la pendiente y (b) es la intersección con el eje y. ¿Por qué es importante esto? Porque la pendiente nos dice cuán inclinada está la recta, y esto es clave para determinar su posición relativa con respecto a otra recta.
## Tipos de Posición Relativa
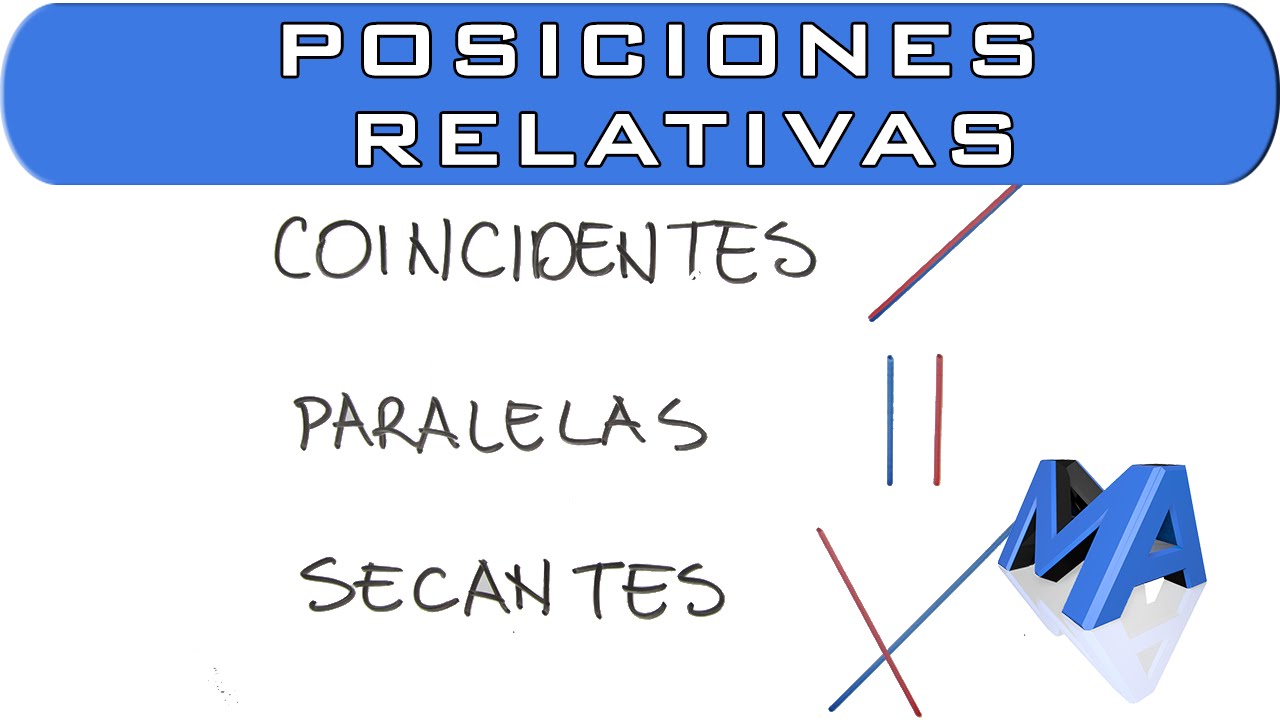
Cuando hablamos de la posición relativa de dos rectas, hay tres situaciones posibles:
1. Rectas paralelas: Nunca se cruzan. Tienen la misma pendiente, pero diferentes intersecciones.
2. Rectas coincidentes: Son la misma recta, lo que significa que todos los puntos de una recta son también puntos de la otra.
3. Rectas secantes: Se cruzan en un solo punto. Tienen diferentes pendientes.
Ahora, analicemos cada una de estas situaciones más a fondo.
### Rectas Paralelas
Imagina que estás en una carretera y ves que hay dos carriles que nunca se cruzan, incluso si se extienden hacia el horizonte. Eso es exactamente lo que ocurre con las rectas paralelas. Matemáticamente, esto se traduce en que las pendientes son iguales. Por ejemplo, si tienes dos rectas:
– Recta 1: (y = 2x + 3)
– Recta 2: (y = 2x – 5)
Ambas tienen una pendiente de 2, lo que significa que son paralelas. Sin embargo, sus intersecciones con el eje y son diferentes, lo que las mantiene separadas.
### Rectas Coincidentes
Ahora, hablemos de las rectas coincidentes. Imagina que dibujas una línea sobre otra línea, exactamente en la misma dirección. En este caso, no hay un solo punto donde se crucen, porque son la misma línea. En términos matemáticos, esto ocurre cuando ambas ecuaciones son idénticas. Por ejemplo:
– Recta 1: (y = 3x + 1)
– Recta 2: (2y = 6x + 2) (si simplificamos, resulta en (y = 3x + 1))
Aquí, ambas ecuaciones representan la misma recta, lo que significa que todos los puntos son comunes.
### Rectas Secantes
Finalmente, tenemos las rectas secantes, que son las más emocionantes, porque ¡se cruzan! Imagina dos caminos que se encuentran en un cruce. Para determinar si dos rectas son secantes, basta con comprobar si sus pendientes son diferentes. Por ejemplo:
– Recta 1: (y = x + 2)
– Recta 2: (y = -x + 1)
Aquí, la primera tiene una pendiente de 1 y la segunda tiene una pendiente de -1. Como son diferentes, sabemos que se cruzan en un punto.
## Cómo Determinar la Posición Relativa
Ahora que conocemos los tipos de posición relativa, ¿cómo podemos determinar cuál es la relación entre dos rectas dadas? Hay un par de métodos sencillos que podemos usar.
### Método de las Pendientes
El método más directo es comparar las pendientes de las rectas. Recuerda que si son iguales, son paralelas; si son idénticas, son coincidentes; y si son diferentes, son secantes.
1. Encuentra la pendiente de cada recta.
2. Compara las pendientes.
### Método de la Intersección
Otro enfoque es resolver el sistema de ecuaciones formado por las dos rectas. Si encuentras una solución única, las rectas son secantes. Si no hay solución, son paralelas. Y si hay infinitas soluciones, son coincidentes.
#### Ejemplo Práctico
Vamos a aplicar lo que hemos aprendido. Supongamos que tenemos las siguientes rectas:
– Recta 1: (y = 2x + 4)
– Recta 2: (y = 2x – 3)
Primero, observamos que ambas tienen la misma pendiente (2). Así que, según nuestro análisis, podemos concluir que son paralelas.
Ahora, probemos con otro ejemplo:
– Recta 1: (y = 3x + 1)
– Recta 2: (y = -3x + 2)
Aquí, las pendientes son diferentes (3 y -3). Así que, definitivamente, estas rectas son secantes.
## Gráficos de las Rectas
Ver estas rectas en un gráfico puede ser de gran ayuda para entender visualmente su posición relativa. Al graficar las ecuaciones, podrás observar claramente si se cruzan, son paralelas o coinciden.
### Herramientas para Graficar
Hoy en día, existen muchas herramientas y aplicaciones en línea que te permiten graficar ecuaciones de forma sencilla. Puedes utilizar herramientas como Desmos o GeoGebra para experimentar y ver cómo cambian las rectas cuando alteras sus ecuaciones.
## Aplicaciones en la Vida Real
Entender la posición relativa de las rectas no es solo un ejercicio académico. Tiene aplicaciones prácticas en diversos campos. Por ejemplo, en arquitectura, los arquitectos deben considerar cómo las diferentes estructuras se intersecarán o se alinearán. En el diseño gráfico, es esencial para crear composiciones equilibradas. ¿Te imaginas un puente que no considere estas relaciones? ¡Sería un desastre!
## Conclusión
En resumen, estudiar la posición relativa de dos rectas es un concepto fundamental en geometría que tiene aplicaciones en la vida cotidiana. Ya sea que estés resolviendo problemas matemáticos o aplicando este conocimiento en el mundo real, entender cómo funcionan las rectas puede abrirte muchas puertas. Así que la próxima vez que te encuentres con dos rectas, recuerda todo lo que has aprendido aquí y trata de determinar su relación. ¡Es un ejercicio que vale la pena!
## Preguntas Frecuentes
1. ¿Qué sucede si las rectas tienen la misma pendiente y la misma intersección?
– En ese caso, las rectas son coincidentes.
2. ¿Cómo puedo saber si dos rectas son paralelas sin graficarlas?
– Solo necesitas comparar sus pendientes; si son iguales, las rectas son paralelas.
3. ¿Es posible que dos rectas se crucen en más de un punto?
– No, dos rectas en un plano solo pueden cruzarse en un solo punto o ser coincidentes.
4. ¿Cómo afectan las intersecciones en la resolución de problemas del mundo real?
– Las intersecciones son cruciales en la planificación urbana y la ingeniería, donde se necesita entender cómo se cruzan diferentes elementos.
5. ¿Qué herramientas puedo usar para practicar más sobre este tema?
– Puedes utilizar aplicaciones como Desmos o GeoGebra para graficar y experimentar con diferentes ecuaciones de rectas.
¡Espero que esta guía te haya resultado útil! Ahora, ¿estás listo para aplicar este conocimiento y ver cómo se relacionan las rectas en tu vida cotidiana?