Cuando hablamos de estadística, los cuartiles son herramientas esenciales para entender la distribución de un conjunto de datos. Imagina que estás organizando una fiesta y quieres saber cuántos amigos estarán en cada grupo de edad. Los cuartiles te ayudarán a dividir esos datos en partes más manejables. En este artículo, vamos a desglosar el proceso de cálculo de los cuartiles de manera sencilla y clara, paso a paso, para que puedas aplicarlo a cualquier conjunto de datos que necesites analizar. ¡Vamos a sumergirnos en el mundo de los cuartiles!
¿Qué son los Cuartiles?
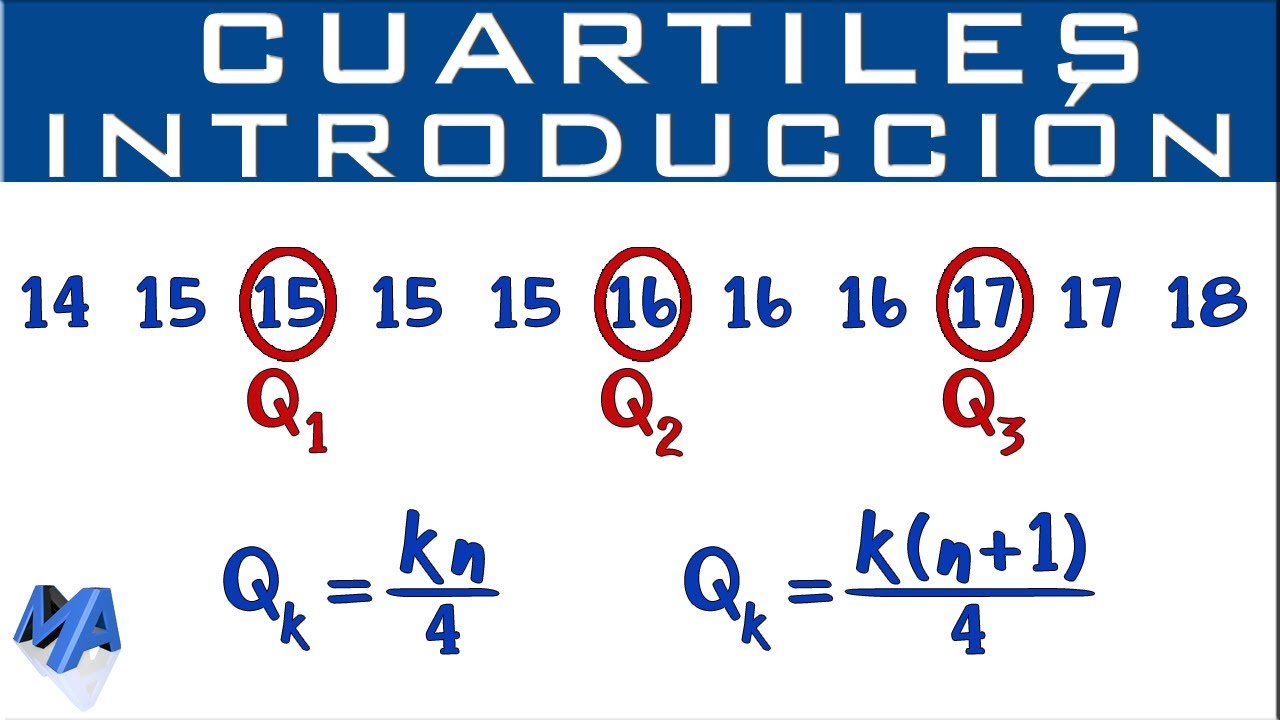
Antes de entrar en materia, es crucial entender qué son los cuartiles. Los cuartiles son valores que dividen un conjunto de datos en cuatro partes iguales. En otras palabras, si tienes un conjunto de datos ordenados, el primer cuartil (Q1) es el valor que separa el 25% inferior de los datos del 75% superior. El segundo cuartil (Q2) es simplemente la mediana, que divide el conjunto en dos mitades. Finalmente, el tercer cuartil (Q3) separa el 75% inferior del 25% superior. ¡Así de simple! Pero, ¿cómo se calculan? Vamos a verlo paso a paso.
Pasos para Calcular los Cuartiles
Paso 1: Organizar los Datos
El primer paso en el cálculo de los cuartiles es asegurarte de que tus datos estén organizados. Esto significa que debes ordenarlos de menor a mayor. Por ejemplo, si tienes los siguientes números: 12, 5, 8, 20, 15, primero los ordenarías así: 5, 8, 12, 15, 20. ¿Ves la diferencia? Ahora tus datos son más fáciles de manejar. Recuerda, ¡el orden es clave!
Paso 2: Calcular la Mediana (Q2)
Una vez que tus datos están ordenados, el siguiente paso es encontrar la mediana, que es el segundo cuartil (Q2). Si tienes un número impar de datos, la mediana es el valor del medio. Por ejemplo, si tus datos son 5, 8, 12, 15, 20, la mediana sería 12, porque es el número del medio. Pero si tu conjunto de datos tiene un número par de elementos, digamos 5, 8, 12, 15, 20, 25, debes tomar los dos valores del medio (12 y 15), sumarlos y dividirlos por 2. Así que Q2 sería (12 + 15) / 2 = 13.5. ¿Ves cómo cambia el juego?
Paso 3: Encontrar el Primer Cuartil (Q1)
Ahora que tienes la mediana, es hora de encontrar el primer cuartil (Q1). Q1 es la mediana del primer 25% de los datos. Para hacer esto, solo necesitas observar los datos que están por debajo de Q2. En nuestro ejemplo anterior, los datos son 5 y 8. Así que Q1 sería la mediana de 5 y 8. Dado que hay dos números, sumamos 5 y 8, y dividimos por 2, obteniendo (5 + 8) / 2 = 6.5. ¡Listo! Ya tenemos Q1.
Paso 4: Calcular el Tercer Cuartil (Q3)
Finalmente, llegamos al tercer cuartil (Q3). Este es un poco más fácil porque solo necesitas mirar los datos que están por encima de Q2. Siguiendo nuestro ejemplo, los datos que quedan son 15 y 20. Así que Q3 sería la mediana de 15 y 20. Al igual que antes, sumamos y dividimos: (15 + 20) / 2 = 17.5. ¡Y voilà! Ahora tenemos Q3 también.
Ejemplo Práctico
Para que todo quede más claro, vamos a revisar un ejemplo completo. Supongamos que tienes las siguientes puntuaciones de un examen: 45, 67, 89, 23, 78, 90, 56, 75. Sigamos los pasos que hemos aprendido.
Organizar los Datos
Primero, organizamos los datos: 23, 45, 56, 67, 75, 78, 89, 90.
Calcular la Mediana (Q2)
Con 8 datos, la mediana es el promedio de los dos valores del medio, que son 67 y 75. Así que Q2 = (67 + 75) / 2 = 71.
Encontrar el Primer Cuartil (Q1)
Ahora, miramos los datos inferiores a la mediana: 23, 45, 56, 67. La mediana de estos cuatro números es (45 + 56) / 2 = 50.5, por lo que Q1 = 50.5.
Calcular el Tercer Cuartil (Q3)
Finalmente, miramos los datos superiores a la mediana: 75, 78, 89, 90. La mediana de estos números es (78 + 89) / 2 = 83.5, así que Q3 = 83.5.
Interpretando los Cuartiles
Una vez que hayas calculado Q1, Q2 y Q3, puedes comenzar a interpretar lo que estos números significan en el contexto de tus datos. Por ejemplo, si Q1 es 50.5 y Q3 es 83.5, esto indica que el 50% de los estudiantes obtuvo una puntuación entre estos valores. Esto te da una idea clara de cómo se distribuyen las puntuaciones y dónde se encuentran los puntos extremos. Es como mirar un mapa que te muestra dónde están tus amigos en la fiesta: algunos están en la pista de baile (los más altos) y otros en la zona de descanso (los más bajos).
Aplicaciones de los Cuartiles
Los cuartiles tienen aplicaciones en muchos campos, desde la educación hasta el análisis financiero. Por ejemplo, en educación, pueden ayudarte a entender cómo se desempeñan los estudiantes en un examen en comparación con sus compañeros. En el mundo de los negocios, los cuartiles son útiles para analizar ingresos, costos y otras métricas clave. Es como tener una brújula que te guía a través del vasto océano de datos.
Errores Comunes al Calcular Cuartiles
Como en cualquier proceso, es fácil cometer errores. Aquí hay algunos de los errores más comunes que debes evitar:
- No ordenar los datos: Siempre asegúrate de que tus datos estén en orden. Este es el primer paso y es crucial.
- Confundir la mediana con el promedio: La mediana es diferente del promedio. No los confundas, ya que pueden ofrecerte información distinta.
- No considerar los datos atípicos: A veces, un valor extremadamente alto o bajo puede afectar los cuartiles. Es importante analizarlos en contexto.
¿Los cuartiles son lo mismo que los percentiles?
No exactamente. Los cuartiles dividen los datos en cuatro partes iguales, mientras que los percentiles dividen los datos en cien partes. Es una cuestión de escala, pero ambos son útiles para entender la distribución de los datos.
¿Se pueden calcular cuartiles con datos no numéricos?
Los cuartiles se calculan generalmente con datos numéricos. Sin embargo, puedes asignar valores numéricos a categorías para calcular cuartiles de datos categóricos, aunque esto puede ser menos preciso.
¿Qué pasa si tengo un conjunto de datos muy pequeño?
Incluso con un conjunto de datos pequeño, puedes calcular cuartiles. Sin embargo, la interpretación puede no ser tan significativa, ya que con menos datos, las variaciones pueden ser más notorias.
¿Cómo se relacionan los cuartiles con el rango intercuartílico?
El rango intercuartílico (IQR) es la diferencia entre Q3 y Q1. Te da una idea de la dispersión de los datos. Un IQR pequeño indica que los datos están más concentrados, mientras que un IQR grande sugiere más variabilidad.
Calcular los cuartiles puede parecer un proceso complicado, pero con un poco de práctica y comprensión, se convierte en una herramienta valiosa para analizar datos. Recuerda que no solo se trata de números; se trata de contar una historia a través de ellos. La próxima vez que te enfrentes a un conjunto de datos, no dudes en aplicar estos pasos y descubrir qué te están diciendo realmente. ¡Los cuartiles son tus amigos en el mundo de la estadística!