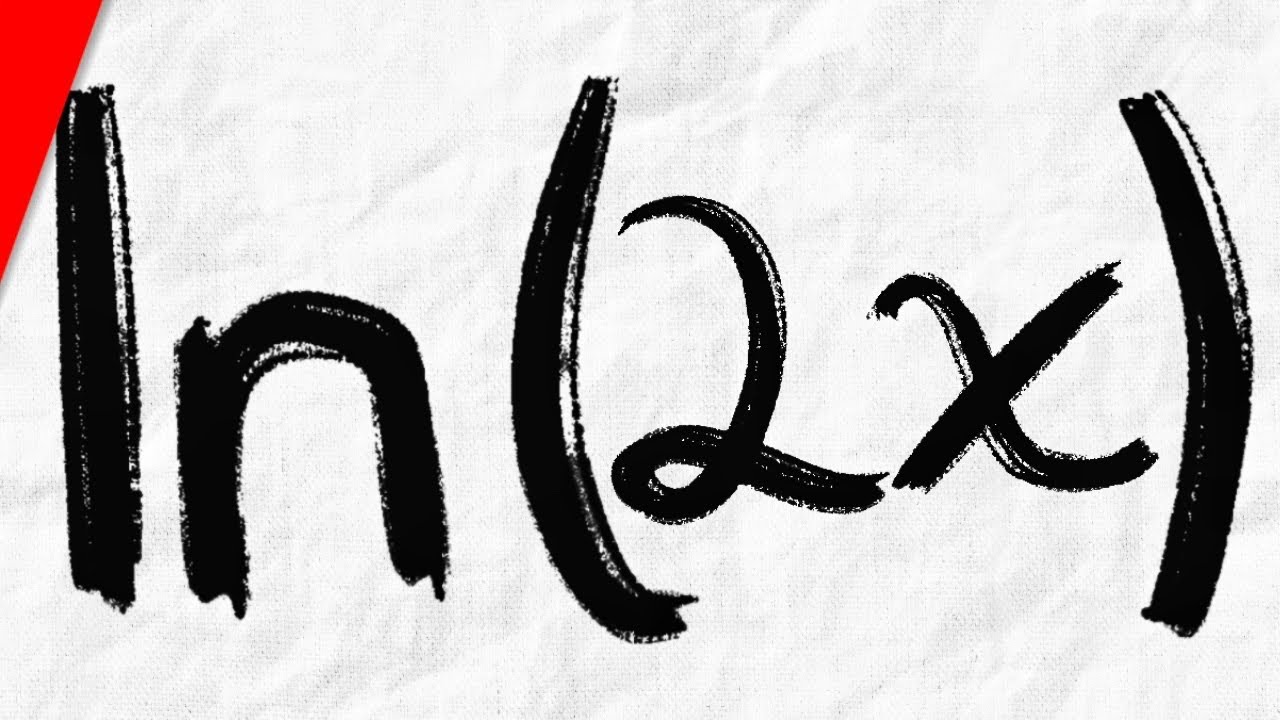Entendiendo la Derivada de ln(2x)
¿Te has encontrado alguna vez con una función que te hace sentir como si estuvieras tratando de descifrar un jeroglífico? Bueno, hoy vamos a desentrañar el misterio de la derivada de ln(2x). Pero no te preocupes, no necesitas ser un genio de las matemáticas para seguirme. Vamos a desglosar este proceso paso a paso, como si estuviéramos armando un rompecabezas. Así que, ¡prepárate para sumergirte en el mundo de las derivadas!
¿Qué es la Derivada?
Antes de que empecemos a calcular, hagamos una breve pausa para entender qué es una derivada. Imagina que estás conduciendo un coche. La derivada te dice cuán rápido estás cambiando tu posición en relación con el tiempo. En el mundo de las funciones matemáticas, la derivada nos dice cómo cambia el valor de una función a medida que cambia su entrada. ¡Sencillo, verdad?
Pasos para Calcular la Derivada de ln(2x)
Paso 1: Identificar la Función
Lo primero que hacemos es identificar nuestra función. En este caso, tenemos ln(2x). ¿Qué significa esto? La función logaritmo natural (ln) es una forma de expresar exponentes, y 2x es simplemente una función lineal. Aquí es donde comienza la diversión.
Paso 2: Aplicar la Regla de la Cadena
Para calcular la derivada de ln(2x), utilizaremos la regla de la cadena. Esta regla es como un superpoder en el mundo de las matemáticas, ya que nos permite derivar funciones compuestas. La regla de la cadena dice que si tienes una función compuesta, la derivada es la derivada de la función exterior multiplicada por la derivada de la función interior. En nuestro caso, la función exterior es ln(u) y la interior es 2x.
Paso 3: Derivar la Función Exterior
Primero, derivamos la función exterior, que es ln(u). La derivada de ln(u) es 1/u. Esto es como decir que si tienes una caja, la forma en que cambia el volumen de la caja depende de su contenido. En nuestro caso, el contenido es 2x. Así que, la derivada de ln(2x) es 1/(2x).
Paso 4: Derivar la Función Interior
Ahora pasamos a la función interior, que es 2x. La derivada de 2x es simplemente 2. Aquí es donde todo comienza a unirse. Ahora tenemos las dos partes necesarias para aplicar la regla de la cadena.
Paso 5: Combinar las Derivadas
Ahora que tenemos la derivada de la función exterior (1/(2x)) y la derivada de la función interior (2), combinamos ambas. Usando la regla de la cadena, multiplicamos: (1/(2x)) * 2. ¡Y voilà! Esto simplifica a 1/x. Y ahí lo tienes, la derivada de ln(2x) es 1/x.
Ejemplo Práctico
Para asegurarnos de que realmente entendemos esto, hagamos un ejemplo práctico. Supongamos que queremos calcular la derivada de ln(4x). Siguiendo los mismos pasos, primero identificamos nuestra función como ln(4x). Aplicamos la regla de la cadena: la derivada de ln(u) es 1/u, así que tenemos 1/(4x). La derivada de 4x es 4. Multiplicando, obtenemos (1/(4x)) * 4, que se simplifica a 1/x. ¡Fácil, verdad?
Visualizando la Derivada
Ahora que hemos calculado la derivada, ¿por qué no visualizarlo? Imagina que estás en un parque de diversiones, subiendo por una montaña rusa. A medida que subes, la pendiente se vuelve más empinada, lo que significa que la derivada está aumentando. Pero cuando desciendes, la pendiente disminuye. Así es como se comporta la derivada: nos muestra cómo cambia la inclinación de la función a medida que avanzamos.
Importancia de la Derivada en la Vida Real
Las derivadas no son solo un concepto matemático abstracto; tienen aplicaciones prácticas en la vida real. Desde la física hasta la economía, la derivada nos ayuda a entender tasas de cambio. Por ejemplo, si estás midiendo la velocidad de un coche, estás utilizando la derivada. Así que, la próxima vez que veas una derivada, recuerda que no es solo un número; es una herramienta poderosa para comprender el mundo que nos rodea.
¿Por qué se utiliza el logaritmo natural en lugar de otros logaritmos?
El logaritmo natural (ln) se utiliza comúnmente porque tiene propiedades únicas que simplifican el cálculo, especialmente en el contexto de las derivadas. Además, se relaciona estrechamente con la función exponencial, lo que lo hace muy útil en diversas aplicaciones matemáticas.
¿Cómo se relaciona la derivada con la integral?
La derivada y la integral son conceptos inversos en cálculo. Mientras que la derivada mide la tasa de cambio, la integral calcula el área bajo la curva de una función. Ambos conceptos están conectados a través del teorema fundamental del cálculo.
¿Puedo usar la regla de la cadena para funciones más complejas?
¡Absolutamente! La regla de la cadena es aplicable a funciones de cualquier complejidad. Cuantas más capas de funciones compuestas tengas, más útil se vuelve esta regla.
¿Es necesario conocer todas las reglas de derivación?
Conocer las reglas básicas de derivación, como la regla de la suma, el producto y la cadena, te facilitará mucho la vida al calcular derivadas. Sin embargo, no es necesario memorizar cada regla; puedes consultarlas cuando sea necesario.
¿Dónde puedo practicar más problemas de derivadas?
Hay muchos recursos en línea donde puedes practicar problemas de derivadas. Sitios web educativos, libros de texto y aplicaciones de matemáticas ofrecen ejercicios y soluciones para ayudarte a mejorar tus habilidades.
Y ahí lo tienes, un viaje completo a través de la derivada de ln(2x). Espero que ahora te sientas más cómodo con el tema y que puedas aplicar estos conceptos en tus futuros estudios. ¡Feliz cálculo!